Dimensions Of Linear Momentum

Introduction: Dimensions Of Linear Momentum

The powers to which the essential units which can be the unrelated units of size are raised for a physical amount so that it will get one unit of that quantity is considered as dimensions of that bodily quantity.

Dimensional Formula

Which represents the dimensional formula of a physical amount and the exponents in this example (a,b,c) are the size.

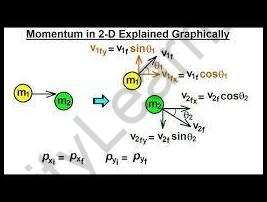
Linear Momentum

From the take a look at Momentum, we know that momentum is the mass of the frame times the speed. So mathematically p= m x v

Change in the momentum of the body stays proportional to the internet pressure and the time over which the internet pressure acts.

Now, we can discover how momentum and internet force are associated.

While studying kinematic equations, you’ve got found out that with constant acceleration, the exchange in speed Δv can also accept as aΔt.

Along these lines, the adjustment of force following a speed increase can be given as-

Δp= mΔv

Therefore, m(aΔt)= FnetΔt

From the above equation, by rearranging the equation to get the cost of Fnet

Given the mass and the internet, force is regular

Fnet= ΔpΔt

From this, we can conclude that the change in momentum is the same as the internet pressure over a time frame.

Now, inertia or translational momentum is defined as linear momentum. Linear momentum does not have a route as it’s miles a vector amount. Also, it needs to be stated that the frame’s momentum is in the equal route as its vector of speed.

The SI unit of straight energy is given as Kg m/s.

The formula for Dimensions of Linear Momentum

Linear Momentum is given by way of –

Linear Momentum = Mass∗Velocity

Dimensions of mass = M

Dimensions of pace = Length Time= L T⁻¹

Therefore,

Dimensions of

Linear Momentum is given via – [M¹ L¹ T^-1]

Where,

M = Mass

L = Length

T = Time

Solved Examples to Calculate Linear Momentum

1. Find the linear momentum of the body having a mass of 10 kg, moving with the rate of 40 m/s.

Solution: Given the mass of the body m= 10 kg

The velocity of the frame v= 4 m/s

Linear momentum is given by-

P = mv

So, Momentum p= 10 x forty

p= 400 kg m/s

2. The linear momentum of a frame of mass five kg is forty kg m/s. What is the speed with which the object is shifting?

Solution: Mass of the body is m= five kg

Given linear momentum of the frame p = forty kgm/s

Linear momentum is given as p= mv

Rearranging the equation, v = pm

So, v = 405

v = eight m/s

Derivation of Dimensions of Linear Momentum

Linear Momentum = Mass × Velocity . . . . . . (1)

The dimensional formula of,

Mass = [M¹ L⁰ T⁰] . . . . (2)

Velocity = [M⁰ L¹ T^-1] . . . . (3)

Let us substitute equation (2) and (3) in equation (1). Hence, we get,

Linear Momentum = Mass × Velocity

Or, L = [M¹ L⁰ T⁰] × [M⁰ L¹ T^-1] = [M¹ L¹ T^-1].

Therefore, the dimensional system for linear momentum may be given using [M¹ L¹ T^-1].

Linear Momentum Dimensions

Linear momentum is a quantity measured by using multiplying the gadget’s mass by its pace. We should realize that a huge and fast-shifting item will have extra momentum than a small and slow-moving object. It is given as p = mv. This way that it is without delay proportional to the mass and speed of the item. When the mass or the speed is extra of the object, then the momentum is wonderful too. The linear momentum conservation is exhibited with the aid of any object in which the momentum amount does not alternate. This amount is a vector amount that has an equal direction to the speed of the item. Its SI unit is composed of kg.M/s.

This quantity became quite crucial for the improvement of classical physics much like the idea of power was. It turned into termed as ‘amount of motion’ because of its significance. Newton gave the second law of motion-based totally on the momentum. He stated that the overall outside pressure is identical to the exchange of momentum inside the machine that is divided by using the time over which the change takes place.

Significance of dimensional formula of the electric field in IIT JEE exam

It is critical to take a holistic approach to every facet of a subject’s chapter. It will not only adequately prepare you for the exam, but will also clarify your understanding of each topic. It will help you in IIT preparation and answer conceptual problems in the exam. The number of questions from the chapter unit and dimensions would be one or two, with a weightage of roughly four marks. You can practice through JEE mock test to get an idea about the weightage of this chapter.

FAQs

. ” image-3=”” headline-4=”h5″ question-4=”What is the dimensional formula for Impulse and linear momentum” answer-4=”I = [M1 L1 T-2] × [T] = [M1 L1 T-1]. Therefore, the impulse is dimensionally represented as [M1 L1 T-1]. ” image-4=”” count=”5″ html=”true” css_class=””]