Table of Contents
Dimensions of Velocity Gradient
Dimensions of Velocity Gradient: The velocity gradient is a measure of how fluid velocity varies between different points within the fluid. The velocity difference between fluid layers adjacent to each other and fluid layers adjacent to each other is called velocity gradient. The velocity difference between adjacent fluid layers is called the velocity gradient and is defined as v/x, where v is the velocity difference and x is the distance between layers.
The momentum transfer rate per unit area between two adjacent fluid layers and between two adjacent fluid layers is proportional to the negative value of the velocity gradient between them. We can also say that the velocity gradient is the velocity rate per unit distance. The potential energy gradient is the rate of change of potential energy per unit distance. Velocity can also be defined as the rate of change of velocity per unit distance, and mathematically it can be deduced that velocity gradient = velocity/distance.
It can also be defined as “the distance travelled by an object in a unit of time”.
The speed of an object is the speed of its position relative to the frame of reference and a function of time. A physical quantity through its basic unit with its dimensions is an expression of the dimensional formula of speed. The dimensional formula of speed is defined as an expression of a physical quantity through its basic unit with its own dimensions.
Dimensions of Velocity Gradient In hydrodynamics:
In hydrodynamics, this is defined as the change in velocity between adjacent fluid layers. Velocity change can refer to differences in velocity between layers of flow in a pipe, and is often used to denote the gradient of the flow’s velocity with respect to its coordinates. It can be defined as the derivative of the strain tensor with respect to time, or as the symmetric component of the gradient (derived from position) of the flow velocity.
Gradients are also defined as the gradients described in the velocity space, called strain rate tensors and vorticity sensors, respectively. The velocity gradient is a space tensor that carries information about the velocity of the vector in the deformed configuration as an object deforms as a function of time. The temperature gradient is a dimensional value expressed in degrees per unit length.
Viscosity:
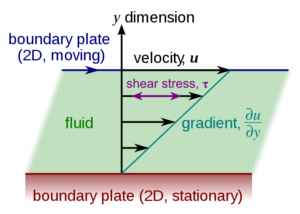
Viscosity is defined as the shear force per unit area required to produce a unit velocity gradient. Angular velocity is defined as the change in angular displacement per unit of time.
Rigid rotation does not change the relative position of fluid elements, so the antisymmetric velocity gradient term R does not affect the rate of change in strain. Under turbulent conditions, the velocity profile is no longer parabolic, but as shown in Fig. For turbulent flow, the average fluid velocity in the pipe is 0.82 x velocity at the centre. It is assumed that the third component of the velocity (outside the screen) is equal to zero everywhere.
Or you can use both strain gradients to calculate the velocity gradient and use it to include or boost in the stress calculation. For example, suppose Abaqus performs a time step during a transient simulation that is Delta t = 0.1. With the help of what is immediately above, one can calculate the Euler quantity bf L using only the Lagrangian quantity, bf F.
Water behaving like a Newtonian fluid:
Water will behave like a Newtonian fluid, which means that there will be a linear relationship between shear stresses (internal forces acting on the water) and shear strain rate (velocity gradient). The curve representing this relationship also contains the origin.
All gradients like velocity gradients, potential gradients, and magnetic field gradients have magnitude and direction, but all gradients like velocity gradients, scalars, because they don’t do not follow vector algebra.
FAQs:
What is the unit of velocity gradient?
1/sec= per second
What is velocity gradient in steady flow?
The rate at which velocity changes as a function of distance from the stationary layer.






