Even Functions

Even odd functions in mathematics seem to be functions that satisfy specific symmetry relations when taking additive inverses. They also seem to be useful in many areas of mathematics, particularly the theory of power series and Fourier series. In different ways, either algebraically or graphically, a function can be defined as even, odd, or neither. The area below the curve has been given by the integral of a function. When solving definite integrals, we use properties of even and odd functions. To do so, we must first understand the integral’s limits and the nature of the function.

An even function is the one whose graph remains unchanged when reflected in the y-axis. Assume f(x) is really a function that is said to be an even function if f(-x) equals f(x).

Take a look at the function f(x), in which x is a real number. Once we substitute -x for x and get the same expression as the original function, we call the function f(x) an even function. Such that, an even function is one in which f(-x) = x for all real values of x.

Even Function Graph

An even function graph is symmetrical about the y-axis. This means that if you were to reflect the graph across the y-axis, the resulting graph would be identical to the original graph. In other words, the shape of the graph is symmetrical about the y-axis.

An even function is one that produces an output that is always even. This means that the function will always produce an output that is a multiple of two. For example, the function f(x) = 2x produces an output that is always even. The function f(x) = x2 produces an output that is always odd.

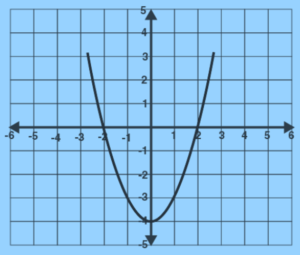
We could see that the graph’s curve is symmetric about the y-axis. That is, we can see the same curved shape if we flip the graph vertically.

Even Function Formula

An even function formula would be simply an expression that aids in determining whether a function is even.

Function f(x) = even if f(-x) = f(x)

Properties of Even Functions

• F(x) + f(x) would be an even function for any function f(x).
• In general, the sum or difference of two even functions is even and the product or division of two even functions is even.
• An even function multiplied by itself yields another even function.
• The derivative of an odd function will be an even function.
• The composition of two even functions and the composition of an even and odd function is even.

FAQs

What are Even Functions in Calculus?

The even functions are said to be the functions that are the same for +ve x-axis and -ve x-axis, or graphically, symmetric about the y-axis. For all x, it is represented as f(x) = f(-x). Even functions include x4, cos x, y = x2, and so on.

Is cos x an Even Function?

The even function equation can be written mathematically as f(x) = f(x) for all x. Once we substitute the value, we get cos(x) = cosx. As a result, cos x is an even function.

Are even functions continuous?

The fact that a function would be odd or even does not imply differentiability or even continuity. The Dirichlet function, for instance, would be even but not continuous.