Table of Contents
The Geometric Mean is an average that uses the product of two integers to explain the typical value of a sequence of numbers. It is commonly used in the fields of statistics and mathematics to determine the mean instead of utilising the standard Arithmetic Mean approach, which does not provide an exact measure of returns like the Geometric Mean.
What does the term “geometric mean” mean?
The geometric mean is a type of average of a group of items, such as products, whose quantification is most commonly employed to determine the comparative analysis or performance results of investment, interest rate, or portfolio. “The nth root product of n integers” is how a geometric mean is defined in mathematics. It works better with percentages that are taken from values, whereas the traditional arithmetic mean works with the values themselves. As a result, the geometric mean becomes a popular method for calculating portfolio performance for a variety of reasons, one of which is that it considers compounding effects.
Key Takeaways/Fun Facts
The more time passes, the more complex compounding develops, and the more precise geometric mean applications become.
The geometric mean is best suited to series with serial correlation, which includes investment portfolios, stock yields, bond returns, and market risk premiums.
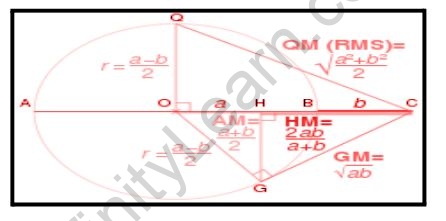
The arithmetic mean (equality bearing only when A=B supposing two values) is always the geometric mean.
The geometric average, which considers year-over-year compounding that steamrolls the average, provides a significantly more accurate estimation of the true return for shaky, erratic figures.
When there are several factors presenting a product and you want to get the “average” factor, the geometric mean is the “way out.”
Distinction Between Arithmetic And Geometric Means
Mean arithmetic
The average of a series of numbers whose sum is divided by the total count of the numbers in the series is known as the arithmetic mean.
(x + y)/2 is the formula.
This can be used in routine calculations with a consistent set of data.
Geometric mean
The compounding effect of the numbers in a series multiplied by taking the nth root of the multiplication is defined as a geometric mean.
It’s written as (xy)(12).
This has financial uses in determining portfolio returns.
Mean and Range in Arithmetic
The Arithmetic Mean (AM), often known as the average in statistics, is the ratio of the sum of all observations to the total number of observations. Outside of statistics, the arithmetic mean can be used to inform or represent concepts. The arithmetic mean can be conceived of as a gravitational centre in a physical sense. The average distance the data points are from the mean of a data set is referred to as standard deviation. In the physical paradigm, the square of standard deviation (i.e. variance) is comparable to the moment of inertia.
The arithmetic mean is a number calculated by dividing the total of a set’s elements by the number of values in the set. So you may use the common phrase Average, or you can be a little fancier and say “Arithmetic mean.” It’s your choice; they both mean the same thing. The arithmetic mean can be either positive or negative.
Arithmetic Mean (Simple) Weighted Arithmetic Mean (Weighted Arithmetic Mean)
Arithmetic Range Range,
as the name implies, is the difference between the data’s largest and smallest value. Using the preceding example as an example, allows us to calculate the range over which the data is scattered. There are ten pupils in the class, and they recently completed a 100-point test. There are two possibilities here.
71, 70, 75, 73, 74, 75, 70, 74, 72,
The gap between the biggest figure, 93, and the smallest value, 48, represents the range in the first scenario.
In the first set, the range is 93 – 48 = 45.
What are the Functions of AM, GM, and HM?
The many forms of means have a wide range of applications in domains such as statistics, mathematics, photography, and biology, among others.
1. Arithmetic Mean: A country’s population’s arithmetic means income is the country’s per capita income.
2. Geometric Mean: A geometric mean is used to compare review scores of different products.
3. Harmonic Mean: In a right triangle, the length of the perpendicular or height (h2) equals half the harmonic mean of a2 and b2.
Is the Geometric Mean superior to the Arithmetic Mean?
When there is a lot of variability in the data set, the geometric mean is better than the arithmetic mean since it is more accurate and effective. As a result, the geometric mean is frequently employed in finance to calculate portfolio returns. When the variables are interdependent, the geometric mean is also used in the scenario.
The theorem of the geometric mean
The right triangle altitude theorem, also known as the geometric mean theorem, is a result in elementary geometry that describes the relationship between the lengths of the hypotenuse altitude and the two-line segments it forms. It states that the altitude is equal to the geometric mean of the two segments.
FAQs
What does it mean to have a geometrical average?
Average Geometric. The geometric mean, also known as the geometric average, takes into account the compounding that occurs over time. Multiplying a set of integers together and raising the result to the inverse of the series' length yields the geometric mean.
What is the geometric mean of the number three?
For example, the geometric mean of a pair of numbers such as 3 and 1 is (31) = 3 = 1.732. In other terms, the geometric mean is defined as the nth root of the product of n numbers. The geometric mean differs from the arithmetic mean, as may be seen.









