Table of Contents
A body begins to rotate about a fixed axis in rotational motion. Thus every particle in the body moves in a circle with linear velocity, i.e. with angular acceleration. The moment of inertia of a body is really the property that causes it to resist angular acceleration. It really is calculated as the sum of the products of the mass of each particle in the body and the square of its distance from the axis of rotation.
A moment of inertia, as well known as the angular mass or rotational inertia, is really a quantity that determines the amount of torque required for a desired angular acceleration or a property of a body that resists angular acceleration. The moment of inertia would be affected by the distribution of mass around the axis of rotation. The MOI depends greatly on the axis position chosen. That really is, the same item may have a different moment of inertia values depending on the location and direction of the axis of rotation.
Calculation of Moment of Inertia
An object’s moment of inertia is indeed a calculated measurement for a rigid body rotating around a fixed axis. The axis could be internal or external, and it may or may not be fixed. The moment of inertia (I) has been, however, always described in relation to that axis.
The moment of inertia has been calculated as the “sum of the product of mass” of each particle multiplied by the “square of its distance from the axis of rotation.” The Moment of Inertia formula would be written as
I = Σ miri2
The moment of inertia is often known as the angular mass or rotational inertia.
kg m2 would be the SI unit for a moment of inertia.
Example: Moment of Inertia of a Uniform Rod about a Perpendicular Bisector
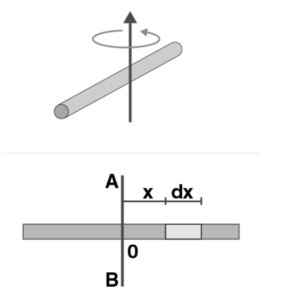
Let’s consider a uniform rod of mass M and length L, and calculate the moment of inertia about the bisector AB. The origin has been set to zero.
The mass element ‘dm’ under consideration has been located between x and x + dx from the origin.
Due to the uniformity of the rod, the mass per unit length (linear mass density) remains constant.
M/L = dm/dx
dm = (M/L)dx
Now, the moment of inertia of dm is,
dI = dm x2
dI = (M/L) x2.dx
I =-L/2 ∫+L/2 dI = M/L × -L/2∫+L/2 x2 dx
In which, x = -L/2 is the left end of the rod and ‘x’ changes from –L/2 to +L/2, the element covers the entire rod.
I = M/L × [x3/3]+L/2-L/2
I = ML2/12.
Hence, the moment of inertia of a uniform rod about a perpendicular bisector (I) = ML2/12.
FAQs
Why do we calculate the moment of inertia?
The MOI of an item helps determine how much torque is required to achieve a given angular acceleration. While trying to calculate torque or rotational force, the mass MOI must be known.
What factors determine the moment of inertia of a solid disk pulley?
The moment of inertia of a body has always been determined by its mass, and it is also calculated by how that mass is distributed relative to the axis of rotation.





