Table of Contents
Circle Definition:
A circle is a closed two-dimensional object in which all points in the plane are equidistant from a single point known as the “centre.” The line of reflection symmetry is formed by every line that travels through the circle. For any angle, it also exhibits rotational symmetry around the centre. In the plane, the circle formula is as follows:
(x-h)2 + (y-k)2 = r2
where (x,y) are the coordinate points
(h,k) is the coordinate of the centre of a circle
and r is the radius of a circle.
Circle Area Proof:
We know that Area is the space occupied by the circle.
Consider a concentric circle having an external circle radius to be ‘r.’ Open all the concentric circles to form a right-angled triangle. The outer circle would form a line having a length 2πr forming the base.
The height would be ‘r’
Therefore the area of the right-angled triangle formed would be equal to the area of a circle.
Area of a circle = Area of triangle = (1/2) ×b ×h
= (1/2) × 2π r × r
Therefore, the Area of a circle = πr2
Circles’ Characteristics:
The following are some of the most important basic features of circles:
- A circle’s outer line is equidistant from its centre.
- The circle’s diameter divides it into two equal sections.
- Circles with equal radii are congruent with one another.
- Varying-sized circles or circles with different radii are comparable.
- The greatest chord in the circle is the diameter, which is double the radius.
Circle Formulas:
- Area of a Circle Formula: The area of a circle refers to the amount of space covered by the circle. It totally depends on the length of its radius → Area = πr2 square units.
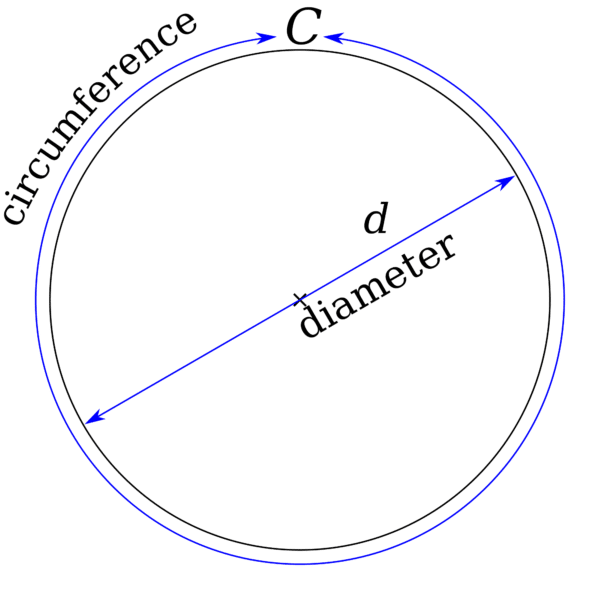
- Circumference of a Circle Formula: The circumference is the total length of the boundary of a circle → Circumference = 2πr units.
- Arc Length Formula: An arc is a section (part) of the circumference. Length of an arc = θ × r. Here, θ is in radians.
- Area of a Sector Formula: If a sector makes an angle θ (measured in radians) at the centre, then the area of the sector of a circle = (θ × r2) ÷ 2. Here, θ is in radians.
- Length of Chord Formula: It can be calculated if the angle made by the chord at the centre and the value of radius is known. Length of chord = 2 r sin(θ/2). Here, θ is in radians.
- Area of Segment Formula: The segment of a circle is the region formed by the chord and the corresponding arc covered by the segment. The area of a segment = r2(θ − sinθ) ÷ 2. Here, θ is in radians.
FAQs
What is the radius and diameter of a circle?
The radius of a circle is the line segment that connects the centre point and the circle surface. The diameter is considered the longest chord of a circle which is twice the radius.
What is a chord of a circle?
The chord of a circle is defined as the straight line segment whose both endpoints touch the surface of a circle. The longest chord of a circle is a diameter.



