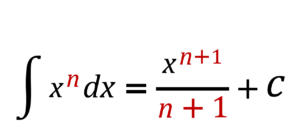Table of Contents
Introduction
The computation of an integral is known as integration. Integrals are used in mathematics to calculate a variety of useful quantities such as areas, volumes, displacement, and so on. When we talk about integrals, we typically mean definite integrals. Antiderivatives are computed using indefinite integrals. Apart from differentiation, integration is one of the two major calculus subjects in mathematics (which measure the rate of change of any function with respect to its variables). It’s a broad topic that’s covered in upper-level classes like Classes 11 and 12. The integration of parts and the substitution of parts is covered in detail. You will study the definition of integrals in mathematics, as well as integration formulae and examples.
Definition of Integration
The accumulation of discrete data is referred to as integration. The integral is used to determine the functions that will characterize the area, displacement, and volume that result from a collection of little data that cannot be measured individually. In a wide sense, the concept of limit is employed in calculus to construct algebra and geometry. Limits assist us in analyzing the outcome of points on a graph, such as how they go closer to each other until their distance is nearly zero. There are two primary forms of calculus that we are familiar with —
- Calculus of Differences
- Calculus of Integrals
Integration is a notion that has evolved to handle the following sorts of problems:
- When the derivatives of the problem function are known, find it.
- Under specific constraints, determine the region limited by the graph of a function.
These two issues led to the creation of the “Integral Calculus,” which consists of both definite and indefinite integrals. The Fundamental Theorem of Calculus connects the concepts of differentiating and integrating functions in calculus.
Integration in Mathematics
Integration is a way of finding the total by adding or summing the components. It’s a reversal of differentiation, in which we break down functions into pieces. This approach is used to calculate the total on a large scale. Calculating little addition problems is a simple operation that may be done manually or with the aid of calculators. Integration methods, on the other hand, are utilized for large addition problems where the bounds might reach infinite. Calculus is divided into two parts: integration and differentiation. These subjects have a very high idea level. As a result, it is first exposed to us in high school and later in engineering or further education.
FAQ’S
What are some examples of real-world integration applications?
Integrations are essential for calculating the center of gravity and mass, as well as predicting the positions of planets and other celestial bodies.
What is the definition of calculus' basic theorem?
Calculus' fundamental theorem connects the concepts of differentiation and integration.
In Math, distinguish between two types of integrals.
The integral assigns a number to a function, and integration is one of the two major ideas in mathematics. Definite and indefinite integrals are the two types of integrals.
What exactly is the point of integration?
Many items employ integration to discover their volume, area, and core values.