Important Topic: Vectors

Introduction:

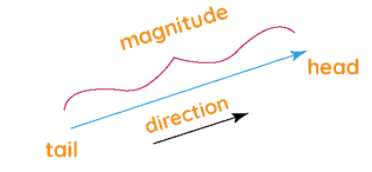
Vectors are geometrical entities that have magnitude and direction. A vector can be represented as a line with an arrow pointing towards its direction and its length represents the magnitude of the vector. The concept of vectors was evolved over a period of 200 years.

Further, the use of vectors started in the late 19th century with the advent of the field of electromagnetic induction. Here, we will discuss the definition of vectors along with properties of vectors, formulas of vectors, and operation of vectors along using solved examples for a better understanding.

Definition of Vector:

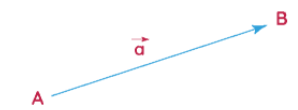
A vector is a Latin word that means carrier. Vectors carry a point A to point B. The length of the line between the two points A and B is called the magnitude of the vector and the direction of the displacement of point A to point B is called the direction of the vector AB. Vectors are also called Euclidean vectors or Spatial vectors. Vectors have many applications in Maths, physics, engineering, and various other fields.

Example: Vectors play an important role in physics. For example, velocity, displacement, acceleration, force are all vector quantity that have a magnitude as well as a direction.

Representation of vector:

Vectors are represented by bold lowercase such as a or using an arrow over the letter such as . Vectors can also be denoted by their initial and terminal points with an arrow above them, for example, vector AB can be denoted as The standard form of representation of a vector is . Here, a, b, c are scalar values and are the unit vectors along the x-axis, y-axis, and z-axis respectively.

The initial point of a vector is also called the tail whereas the terminal point is called the head. Vectors describe the movement of an object from one place to another. In the cartesian coordinate system, vectors can be denoted by ordered pairs. Similarly, vectors in ‘n’ dimensions can be denoted by an ‘n’ tuple. Vectors are also identified with a tuple of components which are the scalar coefficients for a set of basis vectors. The basis vectors are denoted as: e1 = (1,0,0), e2 = (0,1,0), e3 = (0,0,1)

Magnitude of Vectors:

The magnitude of a vector can be calculated by taking the square root of the sum of the squares of its components. If (x, y, z) are the components of a vector A, then the magnitude formula of A is given by, The magnitude of a vector is a scalar value.

Angle between two vectors:

The angle between two vectors can be calculated using the dot product formula. Let us consider two vectors a and b and the angle between them to be θ. Then, the dot product of two vectors such as a·b = |a||b| cosθ. We need to determine the value of the angle θ such as

θ = cos^-1[(a·b)/|a||b|]

Types of Vectors:

Let us define a few types of vectors and their properties:

• Zero Vectors:-Vectors that have 0 magnitude are called zero vectors, denoted by = (0,0,0). This vector has zero magnitudes and no direction. It is also called the additive identity of vectors.
• Unit Vectors:-Vectors that have magnitude equals to 1 are called unit vectors, denoted by â . It is also called the multiplicative identity of vectors. The magnitude of a unit vectors is 1. It is generally used to denote the direction of a vector.
• Position vectors:- Position vectors are used to determine the position and direction of movement of the vectors in a three-dimensional space. The magnitude and direction of position vectors can be changed. It is also called the location vector.
• Equal Vectors:- Two or more vectors are said to be equal if their corresponding components are equal. Equal vectors have the same magnitude as well as direction.
• Negative Vector:- A vector is said to be the negative of another vector if they have the same magnitudes but opposite directions. If vectors A and B have equal magnitude but opposite directions, then vector A is said to be the negative of vector B.
• Parallel Vector:- Two or more vectors are said to be parallel vectors if they have the same direction but not necessary the same magnitude. The angles of the direction of parallel vectors differ by zero degrees. The vectors whose angle of direction differs by 180 degrees are called antiparallel vectors, that is, antiparallel vectors have opposite directions.
• Orthogonal Vectors:- Two or more vectors in space are said to be orthogonal if the angle between them is 90 degrees such as
• a·b = |a|·|b|cos90° = 0.
• co-initial vectors:- Vectors that have the same initial point are called co-initial vectors.

Make your IIT Dream come true with Infinity Learn

FAQs

Question: Find the angle between the two vectors and ?

Answer: Given two vectors a = and b =

We need to determine the angle between the vectors a and b using the formula cosθ = a.b / |a||b|

What are Vectors in Math?

The physical quantities that are specified completely by the magnitude and direction are called vector quantities. For example, physical quantities like displacement, velocity, position, force, torque, etc are vector quantities.

What is the difference between vector and scalar?

A scalar is a quantity that does not depend on direction whereas a vector is a physical quantity that has magnitude as well as direction. Examples of scalar are distance, speed, time, etc. Example of vector are displacement, velocity, acceleration, force, etc.

Infinity Learn App

Now you can find answers to all your subject queries & prepare for your Exams on our Educational App – Infinity Learn.