Logarithms Properties

A Brief Outline

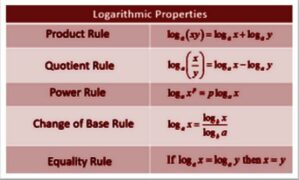
The rules of logarithms, which are derived from exponent rules, are the properties of the log. These logarithmic features are used to simplify logarithmic statements and solve logarithmic problems.

Important Concepts

Logarithms’ product Property

The sum of logs is used to indicate the logarithm of a product using the product property of logarithms. The product attribute is deduced as follows: log_a mn = log_a m + log_a n.

Logarithms’ Quotient Property

The difference of logs is used to define the logarithm of a quotient using the quotient property of logarithms. The quotient property is defined as log_a m/n = log_a m – log_a n.

Logarithms’ Power Property

The logarithm’s power property states that log_a mn = n log_a m. It signifies that the argument’s exponent can be dragged in front of the log.

Changes to base Logarithms’ Property

log_b a = (log_c a) / (log_c b) is the change of base property. It indicates that log_b an is the quotient of two natural logarithms (log a)/ (log b), where both logs must have the same base (say c). We know that the calculator has two buttons for evaluating logarithms. The first is log (base 10) and the second is ln (base ‘e’). What if we need to compute a logarithm with a different base, such as log5 2? This characteristic comes in handy when calculating logarithms.

Significance of logarithms properties in IIT JEE exam

Since there are questions in JEE MAINS and ADVANCE based on logarithms, you must have a thorough understanding of how to use the log and its graph because its fundamentals will always be present in problems. However, the topic only amounts to 3% of the total, with only one or two questions.

FAQs

Q. What is a logarithmic function’s parent function?

Ans: The features of exponential functions are explored using logarithms, and exponential functions are solved using logarithms. In calculus, finding the parent of logarithmic functions is useful for calculating the slope of certain functions as well as the area limited by certain curves.

Q. What is the appearance of a logarithmic function?

Ans: The inverse of the exponential function, the logarithmic function is expressed as “the log, base a, of x.” Because the logarithmic function is the inverse of the exponential function, logarithms can only be expressed in their exponential form.

Q. Is it necessary to learn about Logarithmic Functions?

Ans: Yes, learning Logarithmic Functions is vital because they are a fundamental topic in mathematics. These functions have a connection to exponential functions.