Moment of Inertia of a Hollow Sphere

The Moment of Inertia, as well known as the mass moment of inertia, rotational inertia, or angular mass of a rigid body, is really a quantity that determines the torque needed for a desired angular acceleration around a rotational axis, in the same way, that the mass determines the force required for the desired acceleration. This seems to be entirely dependent on the body’s mass distribution and the axis selected, with larger moments necessitating more torque to change the body’s rate of rotation.

The moment of inertia of a hollow sphere or spherical shell has been frequently calculated using the following formula:

I = MR²

Derivation of Hollow Sphere Formula

 

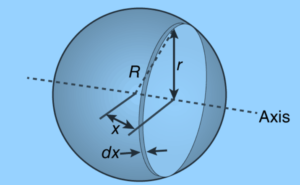
Before we start, let us recall or consider the Moment of Inertia of a Circle, which is given by,

I = mr²

When applying the differential analysis, we get;

dl = r² dm

Then, we need to find the dm value with the formula,

dm = dA

In which A is the total surface area of the shell, which is given as 4πR², and dA is said to be the area of the ring that is formed by differentiation and is expressed as;

dA = R dθ × 2πr

Here R dθ is considered the thickness and 2πr is the circumference of the ring.

Remember that, we get R dθ from the equation of arc length, S = R θ

We have, sin θ = = r = R sinθ

Then, dA becomes as below.

dA = 2πR²sinθ dθ

When substituting the equation for dA into dm, we get,

dm = dθ

At this point, we will substitute the above equation and for ‘r’ into the equation for ‘dI.’ Then we get;

dm = sin³ θ dθ

So, integrating within the limits of 0 to π radians from one end to another, we get;

I = sin³ θ dθ

Then, we need to split sin³θ into two, because it depicts the case of integral of odd powered trigonometric functions. So, we get;

I = sin² θ sin θ dθ

We have, sin² θ is given as sin² θ = 1- cos² θ.

Thus,

I = (1- cos² θ) sin θ dθ

We could use substitution after this, where u = cos θ, we will get;

I = u² – 1 du

We need to carry out the integration as:

I = u² – 1 du,

In this, the integral of u² du = u and the integral of 1 du = u

When substituting the values, we get.

I = {₁^-1 – u₁^-1

I = {[ (-1)³ -1³] − − 1−1}

I = {– −2}

I = { +2}

I = {}

I = x

I = MR²

FAQs

What is a hollow sphere?

A hollow sphere is really a hollowed-out ball with an equal-thickness wall that creates an internal ball within the external ball.

Which among the two spheres is hollow and solid and why?

This cannot be said till the mass is fixed. Both spheres have the same inertia if they have the same mass. And since mass is referred to as inertia, but each has a different moment of inertia. Also because the moment of inertia is always proportional to the distribution mass of the axis on which it is calculated.