Moment of Inertia of Annular Disc

The moment of inertia of a uniform annular disc with mass (m), thickness (t), inner radius (R1), and outer radius (R2) is expressed as;

I = ½ M (R₂² + R₁²)

In this case, we must consider that the disc is rotating about an axis that runs through the centre.

Derivation of Moment of Inertia of Annular Disc

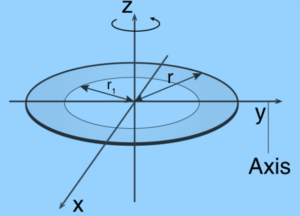
(1) We’ll begin by recalling the moment of inertia expression, which is as follows:

dI = r² dm

In just this case, we can think of dm as the mass of volume dV. The moment of inertia about the z-axis is then considered, yielding the expression;

I_zz = _O∫^R r²dm

The mass dm of the volume element dV, just like relation in a disc, is related to volume and density by;

dm = ρ dV

Then we should compute dV. We would then assume that the disc has a uniform density in this case. In this case, we’ll also consider a ring with radius r, width dr, and thickness t. We might well obtain;

dV = (2 π r dr)t

Once we substitute the values for dm we get;

dm = ρ (2 πt ) r dr

(2) So we can create a new expression for I_zz. It certainly will be;

I_zz = _R1∫^R2 r²dm

I_zz = 2 π ρ t _R1∫^R2 r³dr

Then, we integrate R₁ and R₂. We will now have;

I_zz = 2 π ρ t [R₂⁴/4 – R₁⁴ / 4]

I_zz = (½) π ρ t [ R₂⁴ – R₁⁴] ……………(1)

Even so, we can also express it as [ R₂² + R₁²][ R₂² – R₁²].

Thus, the equation now becomes;

I_zz = ½ πρt [ R₂² + R₁²][ R₂² – R₁²] ……………..(2)

(3) The total mass of the annular disc must now be determined. We would then subtract the total mass (M₂) of a disc of radius R₂ from the mass (M₁) of a disc of radius R₁.

We have, Mass = Density x Area x Thickness

So,

M₂ = π ρ t R₂²

M₁ = π ρ t R₁²

Thus, the mass of the annular disc is given as;

M_a = M₂ – M₁

M_a = π ρ t R₂² – πpt R₁²

M_a = π ρ t (R₂² – R₁²)

(4) The following step will be to substitute the above values in equation 2, which really is.

I_zz = ½ π ρ t [ R₂² + R₁²][ R₂² – R₁²]

After adding the values and integrating them, we could indeed write the expression for an annular disc’s moment of inertia as;

I_zz = ½ M_a (R₂² + R₁²)

FAQs

What is an annular disc?

The annulus fibrosus, a strong outer ligamentous ring, and the nucleus pulposus, an inner jelly-like section, make up these discs. The annulus fibrosus and nucleus pulposus work together to distribute pressure evenly throughout the disc. An annular disc tear is really a rip in the outer ligamentous ring of the disc.

What do you mean by the annular ring?

An Annulus is really a ring-shaped object defined by the circumference of two concentric circles of varying radii. An Annulus seems to be similar to a throw-ring. We can consider this as a circular disc with a circular hole in it.