Newton’s Laws of Cooling

The rate of heat loss of a body is directly proportional to the temperature difference between the body and its surroundings, according to Newton’s law of cooling. The law is frequently qualified by the condition that the temperature difference be small and the nature of the heat transfer mechanism remain constant. As such, it is equivalent to saying that the heat transfer coefficient, which mediates heat losses and temperature differences, is a constant.

This condition is generally met in heat conduction (where it is guaranteed by Fourier’s law), because most materials’ thermal conductivity is only weakly dependent on temperature. Newton’s Law is followed in convective heat transfer for forced air or pumped fluid cooling, where the fluid properties do not vary significantly with temperature, but it is only This is roughly true for buoyancy-driven convection, where the flow velocity increases with temperature difference. Finally, Newton’s law of cooling holds only for very small temperature differences in the case of heat transfer by thermal radiation. When expressed in terms of temperature differences, Newton’s law yields a simple differential equation expressing temperature-difference as a function of time (with several additional simplifying assumptions, such as a low Biot number and a temperature-independent heat capacity). The solution to that equation describes a time-dependent exponential decrease in temperature difference. This characteristic temperature-difference decay is also linked to Newton’s law of cooling.

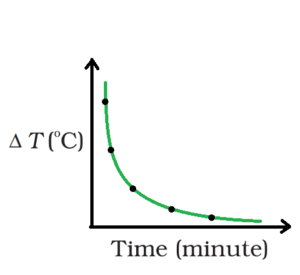
When hot water or milk is left on a table to cool, it does so gradually. It eventually reaches the surrounding temperature. Hot water or milk can be cooled by exchanging heat with the surrounding environment. In this case, the cooling of hot water is determined by the temperature difference between it and its surroundings. The graph shows that the rate of cooling is faster at first, then slows as the body temperature drops. Heat radiation is the process by which a hot body loses heat to its surroundings. The rate of heat loss is determined by the temperature difference between the body and its surroundings.

Overview

Newton’s law of cooling describes the rate at which an exposed body changes temperature through radiation that is approximately proportional to the difference in temperature between the object and its surroundings, assuming the difference is small. According to Newton’s rule of cooling, the rate of heat loss from a body is directly proportional to the temperature differential between the body and its surroundings. According to Newton’s law of cooling, the rate at which an exposed body changes temperature through radiation is approximately proportional to the difference between the object’s temperature and its surroundings, provided the difference is small. According to Newton’s law of cooling, the rate of heat loss from a body is directly proportional to the temperature difference between the body and its surroundings. The rate at which a body exposed to radiation changes its temperature is approximately proportional to the difference between the object’s temperature and its surroundings, and the provided difference is small. Newton’s Law of Cooling is the name given to this phenomenon.

Newton was the first to conduct a systematic analysis of the relationship between the heat lost by a body in a specific enclosure and its temperature. Newton’s law of cooling defines the rate at which an exposed body changes temperature through radiation as being roughly equal to the temperature difference between the item and its surroundings, provided the difference is small. Keep in mind, however, that the difference over here is very small. We can use Newton’s cooling rule to calculate how quickly a substance at a given temperature will cool in any given environment. It also explains how the rate of cooling of an object is affected not only by the temperature differential between the material and its surroundings, but also by the material’s cooling constant.

dT/dt = k(T_t – T_s) is Newton’s law of cooling.

Newton’s Law of Cooling Formula

The greater the temperature difference between the system and its surroundings, the faster heat is transferred, and thus the body temperature changes.
The formula for Newton’s law of cooling is as follows:

T(t) = T_s + (T_o – T_s) e^-kt

Where,

t stands for time, and

Ts = surrounding temperature,

T(t) = temperature of the supplied body at time t

To denotes the body’s initial temperature, while k denotes the constant.

Newton’s Law of Cooling Derivation

When the temperature difference between the body and its surroundings is small, the rate of cooling is directly related to the temperature difference and the surface area exposed.

dQ/dt ∝ (q – q_s)], where q and qs are the temperature of the object and its surroundings, respectively.

Based on the preceding expression

dQ/dt = -k[q – q_s)]

Newton’s law of cooling is represented by this expression. It can be directly deduced from Stefan’s law, which states,

k = [4eσ×θ³_o/mc] A

dθ/dt = -k[θ – θ_o]

where,

qi = the object’s initial temperature, qf = the object’s final temperature.

ln (q_f – q₀)/(q_i – q₀) = kt

(q_f – q₀) = (q_i – q₀) e^-kt

q_f = q₀ + (q_i – q₀) e ^-kt

Limitations of Newton’s Law of Cooling

• The temperature difference between the body and its surroundings must be minimal.
• As a method of heat loss from the body, only radiation should be used.
• A key constraint of Newton’s law of cooling is that the temperature of the surroundings must remain constant while the body cools.

Applications of Newtons Law of cooling

• To calculate how long it will take a warm object to cool down to a specific temperature.
• To determine the temperature of a drink in a refrigerator after a certain amount of time.
• It aids in determining the time of death by comparing the possible body temperature at the time of death with the current body temperature.

FAQs

In terms of physics, what does Newton's Law of Cooling imply?

A body is hotter than its surroundings and cools in proportion to the temperature of its surroundings. As a result, a warm body cools more quickly than a hot body. The same body cools quickly at first, then gradually.

Are Newton's Law of Cooling and the Stefan–Boltzmann Law Related?

Newton's Law of Cooling states that the rate of heat loss by a body due to radiation is directly proportional to the temperature difference between the body and its surroundings, and the temperature difference is less. Newton's Law of Cooling ignores the fact that a body can cool through both radiation and convection; it only considers radiation (a limitation of this Law). The Stefan-Boltzmann law can also be used to derive this law. When the temperature difference is small, Stefan's Law can be replaced by Newton's Law of cooling.