Table of Contents
Eigendecomposition is the factorization of a matrix into a canonical form in linear algebra, where the matrix is represented in terms of its eigenvalues and eigenvectors. This method can only be used to factorise diagonalizable matrices. When factorising a normal or real symmetric matrix, the decomposition is known as “spectral decomposition,” after the spectral theorem. Eigenvectors and eigenvalues are numbers and vectors associated with square matrices, and when combined, they form the eigen-decomposition of a matrix, which analyses its structure. Although the eigendecomposition does not exist for all square matrices, it has an especially simple expression for a class of matrices commonly used in multivariate analysis, such as correlation, covariance, or cross-product matrices. This type of matrices’ eigen-decomposition is important in statistics because it is used to find the maximum (or minimum) of functions involving these matrices. Principal component analysis, for example, is derived from the eigen-decomposition of a covariance matrix and yields the least square estimate of the original data matrix.
Eigenvector is a special type of vector in linear algebra that contains a system of linear equations. Eigenvalues and eigenvectors play an important role in the analysis of linear transformations, such as instability analysis, atomic orbitals, matrix diagonalization, vibration analysis, and many other fields. This section will go over the definition of eigenvectors, vector normalisation, and eigenvector decomposition.
Normalized Eigenvector
We frequently come across computation of normalised eigenvectors in problems involving eigenvectors. A normalized eigenvector is simply an eigenvector with unit length. It can be found by dividing each component of the vector by the vector’s length. As a result, the vector is converted to a vector of length one. The formula for determining the length of a vector is as follows:
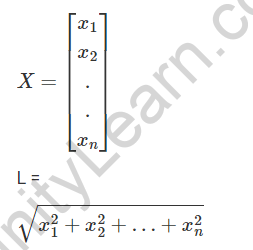
Eigenvector Decomposition
Eigen decomposition is the process of dividing a square matrix A into eigenvalues and eigenvectors. The decomposition of any square matrix into eigenvalues and eigenvectors is always possible as long as the matrix consisting of the given matrix’s eigenvectors is square, as explained in the eigendecomposition theorem. We are all aware that a matrix represents a system of linear equations. The matrix can be worked out to determine its eigenvalues and eigenvectors. Only after the eigenvalues have been computed can the eigenvectors be determined. Eigenvalue decomposition refers to the entire process of determining eigenvectors. It’s also known as eigendecomposition.
FAQs
Were the eigenvectors normalised?
The eigenvectors in V are normalised to have a 2-norm of 1. Demonstrate activity on this post. Eigenvectors can vary by scalar, so a computation algorithm must select a specific scaled value of an eigenvector to display.
Are normalised eigenvectors distinct?
Eigenvectors are NOT one-of-a-kind for a variety of reasons. If the sign is changed, an eigenvector remains an eigenvector for the same eigenvalue. In fact, multiply by any constant and you still have an eigenvector. Different tools may select different normalizations at times.
What is the purpose of eigenvalue decomposition?
In multi-spectral or hyperspectral remote sensing, for example, the Eigen-value Eigen-vector decomposition, or PCA, is used to determine or select the most dominant band/bands. It is used in the design of automobiles, particularly car stereo systems, as well as in the decoupling of three-phase systems.



