Oscillations of a Spring

Oscillation refers to a repetitive movement around a central point, often called the equilibrium point. We commonly use the term “vibration” to describe mechanical oscillations. Everyday examples include the movement of sound waves to our ears and the rhythmic beating of our hearts. Familiar oscillations occur in pendulums, springs, and guitar strings. For instance, a spring moving up and down exhibits oscillatory motion. There are two main types of oscillations: damped and undamped. Alternating current, or AC, represents an example of undamped oscillation.

Oscillations can be further categorized based on their damping level: underdamped (damping constant less than 1), overdamped (damping constant greater than 1), and critically damped (damping constant equal to 1). Damped oscillations are seen in the diminishing swings of a pendulum and the fading vibrations of a tuning fork.

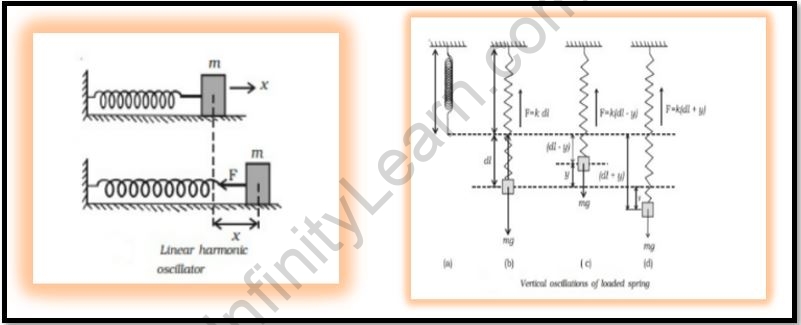
Consider a spring at rest, not subjected to any force. It remains in its natural, or equilibrium, position. When an external force is applied to the spring, it pushes the spring toward this equilibrium point through what is known as a restoring force. Similarly, if the spring is pulled, the restoring force again works to bring it back to equilibrium.

The formula for the spring’s oscillation can be expressed as:

${𝑇}_{𝑠}=2𝜋\sqrt{\frac{𝑚}{𝑘}}$

T_s​=2πkm​​

In this equation,

${𝑇}_{𝑠}$

​ represents the time period of the spring’s oscillation,

$𝑚$

stands for the mass attached to the spring, and

$𝑘$

is the spring constant.

This equation shows that the oscillation period of the spring is directly related to the square root of its mass and inversely related to the square of the spring constant.

We can also observe how a spring moves sideways (horizontal oscillation) and up and down (vertical oscillation).

Also Check: Oscillations

Horizontal Oscillation of Spring

Consider a mass

$𝑚$

connected to one end of a spring, while the other end is fixed to a wall. The entire setup rests on a frictionless surface. Under no external force, the spring stays in its neutral or equilibrium position. But if you pull the spring away from this equilibrium position and then release it, it will snap back towards the equilibrium, indicating that the force which restores it, known as the restoring force, always acts in the opposite direction of the displacement. Additionally, the magnitude of this restoring force is directly proportional to how much the spring is displaced.

The formula for the restoring force is:

$F=-kx$

where

$$

F represents the force,

$$

k is the spring constant, and

$$

x is the displacement from the equilibrium position.

According to Newton’s second law:

$F=ma$

This allows us to express the motion equation as:

$$

ma=−kx

Linking this to the equation of simple harmonic motion, a=−ω²x, we can derive that:

${𝜔}^2=\frac{𝑘}{𝑚}$

ω2=mk​

From which:

$𝜔=\sqrt{\frac{𝑘}{𝑚}}$

ω=mk​​

However, the period

$$

T is calculated by:

$𝑇=\frac{2𝜋}{𝜔}$

T=ω2π​

This gives us the period of the motion:

$𝑇=2𝜋\sqrt{\frac{𝑚}{𝑘}}$

T=2πkm​​

Consequently, the frequency f

$$

is:

$𝑓=\frac{1}{𝑇}=\frac{1}{2𝜋}\sqrt{\frac{𝑘}{𝑚}}$

f=T1​=2π1​mk​​

This formula represents how often the spring oscillates back and forth each second.

Vertical Oscillation of Spring

Consider a setup where two springs are connected one after the other, vertically. At the bottom of one spring, we attach a mass, and the other end of the second spring is fixed to something like a wall. Let’s say the mass moves a total distance of y, which includes the stretches y1 and y2 of the first and second spring, respectively. Assume the springs have stiffness constants k1 and k2. The equations we can derive are:

F = −k1 * y1, and

F = −k2 * y2,

where F is the force that brings the mass back to its original position.

The overall movement is given by:

y = y1 + y2.

The force equation becomes:

−F * (1/k1 + 1/k2).

And simplifying further, we have:

y = – F/k,

which means the equation rearranges to:

−F/k = −F * (1/k1 + 1/k2).

The time period (T) of the motion is:

T = 2π * √(m * (k1 + k2) / (k1 * k2)),

and the frequency (f) is:

f = (1/2π) * √(k1 * k2 / m * (k1 + k2)).

If both springs have the same stiffness constant (k1 = k2 = k), the frequency simplifies to:

f = (1/2π) * √(k / 2m).

Significance of Oscillations of Spring in the IIT JEE exam

The oscillations of a spring play an important role in the IIT JEE exam. The oscillations of a spring are a periodic motion where the object moves back and forth. The object will move a certain distance and then return to its original position. The distance that the object moves is called the amplitude. The time it takes for the object to move back and forth is called the period.

The oscillations of a spring are important in the IIT JEE exam because they are used in many problems. The oscillations of a spring can be used to calculate the period, the amplitude, and the force. The period can be found by using the formula T=2π√(L/g) where L is the length of the spring and g is the gravitational constant. The amplitude can be found by using the formula A=√(F/k) where F is the force and k is the spring constant. The force can be found by using the formula F=ma where a is the acceleration.

The oscillations of a spring are also important because they can be used to solve problems in physics. For example, the oscillations of a spring can be used to solve problems about waves. The oscillations of a spring can also be used to solve problems about energy.

FAQs on Oscillations of a Spring

What does oscillatory motion mean for a spring?

When a mass is moved from its resting position on a spring, it will start to move back and forth in a pattern called harmonic oscillation. This motion can be measured using a coordinate 𝑥 x, representing the position relative to the spring’s new resting point.

What is the basic rule governing spring oscillation?

Springs generally follow Hooke's Law, which states that the force a spring exerts when stretched or compressed is proportional to the extent it is stretched or compressed. This force is described by F=−kx, where 𝑘 is the spring constant, measuring the spring's stiffness in Newtons per meter (N/m).

What is the general formula for oscillation?

The basic oscillations in systems like springs are described by Hooke's Law, 𝐹=−𝑘𝑥 Here, 𝐹 is the force that brings the system back to its equilibrium position, 𝑥 is the displacement from this position, and 𝑘 is the spring's force constant.

Can you give an example of spring oscillation?

An example of spring oscillation is a spring moving up and down. Similarly, electromagnetic waves also oscillate as the electric and magnetic fields expand and contract. This movement represents changes in intensity rather than just positional changes.