Scalar Triple Product

Introduction:

By the name, scalar triple product means the product of three vectors. It gives the scalar value of three vector products. It is used to find the volume of a parallelepiped. In this article, we will study the concept of the scalar triple product, its proof, formula, properties. We will also study the geometric interpretation of the scalar triple product.

Scalar Triple Product:

A scalar triple product gives a scalar value after the product of three vectors. Let a, b, and c be three vectors then the scalar product of vector c with the cross product of vectors b and c. we can represent it as.

[a b c] = (a × b).c

If we have three vectors a, b, and c then we can write the scalar product of these three vectors that can be expressed in many ways.

• a · (b × c)
• a · (c × b)
• b · (a × c)
• b · (c × a)
• c · (b × a)
• c · (a × b)

Also, we need to know about that

• [a, b, c] = a · (b × c) = b · (c × a) = c · (a × b)
• a · (b × c) = – a · (c × b)
• b · (c × a) = – b · (a × c)
• c · (a × b) = – c · (b × a)
• a · (b × c) = (a × b) · c

Formula of scalar triple product:-

Let we have three vectors a, b, and c then we can represent vectors as a = a₁ i + a₂ j + a₃ k, b = b₁ i + b₂ j + b₃ k, and c = c₁ i + c₂ j + c₃ k, then value of vector can can be find with the help of determinant. So the scalar triple product is given by the determinant of the component of three vectors.

So, the formula of the scalar triple product is

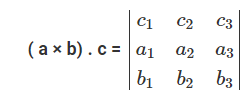
or

Proof of scalar triple product:

Scalar triple product formula represents the volume of parallelepiped whose three sides show the three vectors a, b and c. which is shown as like this figure.

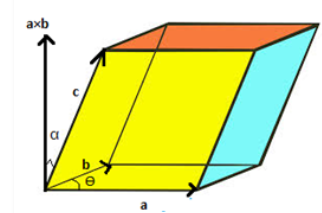
From this figure, the three vectors represent the coterminous edges. In this direction of the cross, the product is perpendicular to the vectors and these cross product of vectors a and b gives the area of the base. We know that volume is the product of area and height. So height is in this case is the component of vector c with the cross product of a and b.

So, if we do denote coterminous edges by three vectors a, b and c then,

Volume of parallelepiped = ( a × b) c cos α = ( a × b) . c

[α is the angle between ( a × b) c cos α = ( a × b) and c]

By the definition of cross product, If we have a = a₁ i + a₂ j + a₃ k, b = b₁ i + b₂ j + b₃ k, and c = c₁ i + c₂ j + c₃ k, then, we can write as

This show the dot product of two vectors. On using the properties of determinants,

( a × b). c =

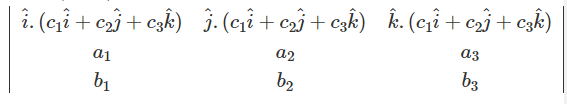
we know that properties of dot product

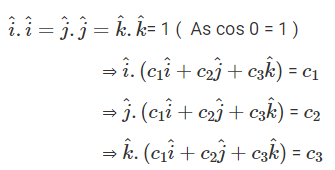
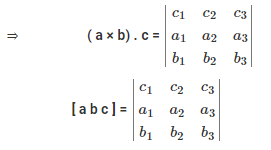
Properties of Scalar Triple Product:

Let us discuss some important properties of the scalar triple product.

• The scalar triple product will be zero if any two vector are parallel to each other such as. [a a b] = 0
• [(a + b) c d] = [a c d] + [b c d] LHS = [(a + b) c d] = (a + b) · (c × d)
  = a · (c × d) + b · (c × d)
  = [a c d] + [b c d] = RHS
• if k is any real number then, [ka b c] = k [a b c], then we can write in its multiple.
• Scalar triple product of non-zero vector will be zero if and only if those vectors are coplanar.
• If the scalar triple product is commutative then, we can write also as

1. a · (b × c) = (b × c) · a

2. b · (c × a) = (c × a) · b

3. c · (a × b) = (a × b) · c

• Scalar triple product is also cyclic in nature, So we can write as

a.(b × c) = b.(c × a) = c.(a × b)

So, also can write as [ a b c ] = [ b c a ] = [ c a b ] = – [ b a c ] = – [ c b a ] = – [ a c b ]

If the triple product of vectors is zero, then it can be inferred that the vectors are coplanar in nature.

The triple product indicates the volume of a parallelepiped. If it is zero, then such a case could only arise when any one of the three vectors is of zero magnitudes. The direction of the cross product of a and b is perpendicular to the plane which contains a and b. The dot product of the resultant with c will only be zero if the vector c also lies in the same plane.

Thus, by the use of the scalar triple product, we can easily find out the volume of a given parallelepiped. There are a lot of real-life applications of vectors that are very interesting to learn.

Make your IIT Dream come true with Infinity Learn

FAQs

Question: Three vectors such as and .

Using of scalar triple product of vectors, verify that [a b c ] = [ b c a ] = – [ a c b ]

Answer: Firstly we will find [ a b c ].[a b c ] = ( a × b ) . c

we know that

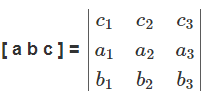
Now, we will find [ b c a ] and [ a c b ]

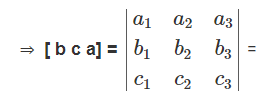
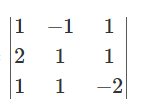
= 1(-2 – 1) + 1(-4 – 1) + 1(2 – 1) = -3 – 5 + 1 = -7

Now, for [ a c b]

= 2(2 – 1) – 1(-2 – 1) + 1(1 + 1) = 2 + 3 + 2 = 7

Hence it proved [ a b c] = [ b c a ] = – [ a c b ]

Question: Define scalar product of two vectors.

Answer: Scalar means given of scalar quantity. In the case of two vectors, we can get scalar quantity if we do the dot product of those vectors. So dot product or scalar product is an algebraic operation that takes the equal-length sequence of numbers and gives a single number. thus, the scalar product of vectors a = [a1, a2, a3,…an] and b = [b1, b2, b3,…, bn] is given by:
a.b = a1b1 + a2b2 + a3b3 + …. + anbn

Question: Why Scalar triple product of three coplanar vectors are zero?

Answer: Let a, b, and c are three non-zero vectors. Then [a, b, c] = 0 if and only if (a × b) · c = 0 ⇔ c is perpendicular to a × b ⇔ c which lie in a plane parallel to both a and b which implies that a, b, and c are coplanar vectors.

Now you can find answers to all your subject queries & prepare for your Exams on our Educational App – Infinity Learn.