Table of Contents
The system of linear equations can be solved by many more methods. Some important methods for solving a system of linear equations are a graphical method, substitution method, elimination method, cross-product method and matrix method. But this method for solving the system of linear equations in 3 or more variable matrix methods is the easiest method. By the matrix method shortest way of solving the linear equation. As compared to the matrix method other methods are more calculative. let we will discuss the method of solving the linear equation by matrix method. the solution to a system of equations and type of equations.
Matrix method:
Solving linear equations using the matrix is done by two prominent methods namely the Matrix method and Row reduction or Gaussian elimination method. In this article, we will look at solving linear equations with matrix and related examples. With the study notes provided below students should develop a clear idea about the topic.
Method of solving Linear Equations using Matrix Method:- Let the equations be:
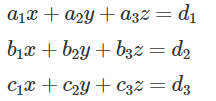
The first method to find the solution to the system of equations is a matrix method. The steps to be followed are:
- All the variables in the equations should be written in the appropriate order.
- The variables, their coefficients and constants are to be written on the respective sides.
Solving a system of linear equations by the method of finding the inverse consists of two new matrices namely
- Matrix A: which represents the variables
- Matrix B: which represents the constants
A system of equations can be solved using matrix multiplication.
We write the above equations in the matrix form as follows
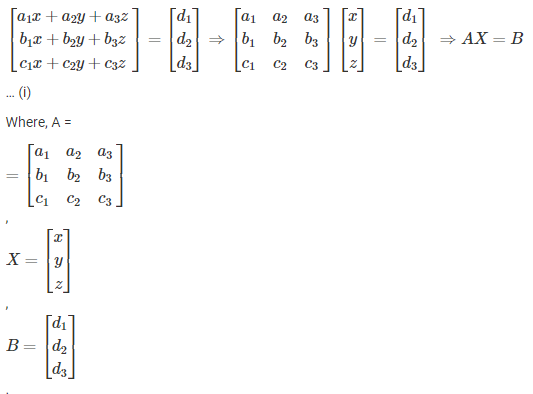
coefficient matrix is A, the variable matrix is X and the constant matrix is B.
Multiplying (i) by A-1 on both sides or can apply cancellation law, then
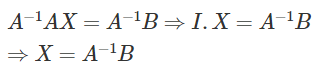
The second method to find the solution for the system of equations is Row reduction or Gaussian Elimination.
- The augmented matrix for the linear equations is written.
- Use elementary such that all the elements below the main diagonal are zero. If a zero is obtained on the diagonal, perform the row operation such that a nonzero element is obtained.
- Back substitution is used to find the solution.
Two main methods for solving the system of the linear equation:
For solving the system of linear equation two matrices such as
Gaussian elimination and Gauss-Jordan elimination.
Processes in beginning for solving the system of the equation of both methods are the
same. To begin solving a system of equations from any method, firstly
changed the equations into a matrix. The coefficient matrix is a matrix comprised of the coefficients of the variables
which is written such that each row represents one equation and each column contains the
coefficients for the same variable in each equation. The constant matrix is the solution to each of the
equations written in a single column and in the same order as the rows of the coefficient matrix.
The augmented matrix is the coefficient matrix with the constant matrix as the last column.
Example: Write the coefficient matrix, constant matrix, and augmented matrix for the
the following system of equations:
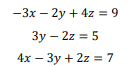
Solution: The coefficient matrix is made by taking the coefficients of each variable and
entering them into each row. The first equation will do write in the first row; the second equation
will do write in the second row, and the third equation will do write in the third row. Also, In the variable matrix the first column
will show the “?” variable; the second column will show the “?” variable and the
third column will show the “?” variable.
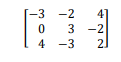
Because the second equation does not contain an “?” variable, a “0” has been entered into
the “?” column in the second row.
The constant matrix will be written in a single-column matrix consisting of the solutions to the equations.
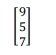
To make the augmented matrix, add the constant matrix as the last column of the
coefficient matrix.
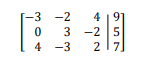
For the Gaussian elimination method, once the augmented matrix will be created, apply elementary
row operations to reduce the matrix to Row-Echelon form. three basic types of
elementary row operations perform the row: (1) row swapping, (2) row multiplication, and (3) row addition. Row
multiplication and row addition can be combined together.
The solution to a System of Equations:
Let us consider a set of values of x, y, z which simultaneously indulge all the equations are known as solutions to the system of equations.
Let us consider, x + y + z = 9
2x – y + z = 5
4x + y – z = 7
Here, values of all the variables in the system of equation x=2,y=3,z=4, is a solution to the system of linear equations.
Because, 2+3+4=9, 4-3+4=5, 8+3-4=7
Also read: Inverse Trigonometric Functions in Maths
FAQs
Q. Solve the following equations by matrix inversion.
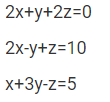
Ans: The system of the above equation can be written in a matrix form such as AX = D and then find A-1 and then we will do multiply it on both sides for solving the above problem.
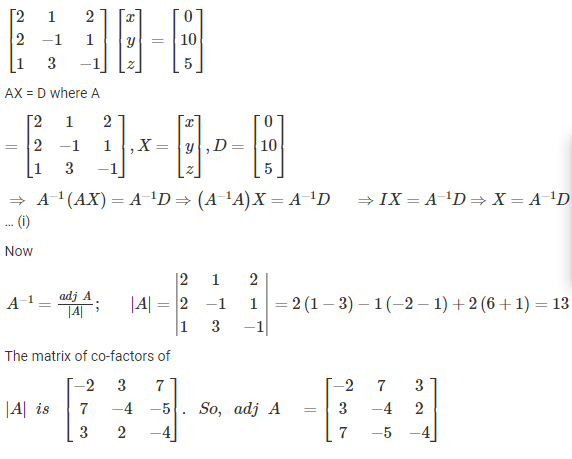
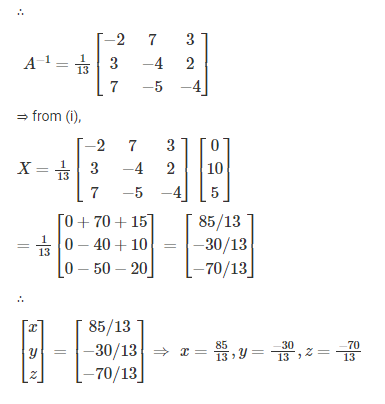
which three matrices do create for solving the system of linear equations?
To begin solving a system of equations with either method, the equations are first changed into a matrix and these matrix names are augmented matrix, coefficient matrix, and constant matrix
What are the two matrix methods for solving the system of a linear equation?
For solving the system of linear equation two methods are Gaussian elimination and Gauss-Jordan elimination.







