Table of Contents
The scientific definition of work differs from its everyday meaning in many ways. Work’s relationship to energy is revealed by the definition of work in physics – whenever work is done, energy is transferred. For work to be done scientifically, a force must be applied and displacement must occur in the direction of the force.
With this in mind, we can say
Work is the product of the component of force in the displacement direction and the magnitude of the displacement.
The preceding statement can be expressed mathematically as follows:
W = (F cos θ) d = F. d
Work done by a variable force
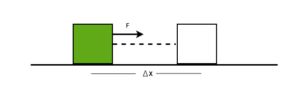
It’s interesting to note that the forces we encounter on a daily basis are mostly variable, which is defined as a variable force. A force is said to perform work on a system if it causes displacement in the system when applied in the force’s direction. When dealing with a variable force, integration is required to calculate the work done. As we know, the work done by a constant force of magnitude F that displaces an object by Δx can be expressed as
W = F.Δx
Work is calculated using integration in the case of a variable force. In the case of a spring, for example, the force acting on any object attached to a horizontal spring can be expressed as:
Fs = -kx
Where k is the spring constant, and x is the displacement of the attached object.
We can see that this force is proportional to the object’s displacement from the equilibrium position, so the force acting at each instant during the spring’s compression and the extension will be different. Thus, in order to calculate the total work done, the infinitesimally small contributions of work done during each instant must be counted.
The integral is calculated as follows:
![]()
Work done by a content force
The work done by a constant force is defined as the product of the object’s displacement (to which the force is applied) and the component of the constant force that is parallel to the direction of displacement.It should be noted that the work done by a constant force is always directly proportional to the product of the magnitude of the applied force and the displacement of the object to which the force was applied.
A force’s work can be divided into two types: work from a constant force and work from a variable force. The magnitude and direction of the force remain unchanged in the first type. Work (W) is equal to force applied (F) multiplied by displacement (x) in this case.
Therefore,
W = F Δx




