Table of Contents
Introduction
Work is defined as the energy transferred to or from an item by applying force and causing a displacement. It is typically depicted as the product of force and displacement in its simplest form. If a force has a component in the direction of the displacement of the site of application, it is said to do positive work. If a force has a component that is away from the axis of dislocation at the point of application, it causes negative work. For example, the work done by the gravitational force on a ball held above the ground and subsequently dropped is equivalent to the mass of the ball (a force) multiplied by the distance to the ground.
A brief outline
Lifting double the weight the same distance or lifting the same weight twice the distance doubles the work. Work and energy are inextricably linked. According to the work-energy principle, a rise in the kinetic energy of a rigid body is ended up caused by an equal amount of positive work performed on the body by the force acting on it. A drop in kinetic energy is created by the resultant force doing an equal amount of negative work. As a result, if the network is positive, the particle’s kinetic energy increases by the work done. If the work done by the network is negative, the particle’s kinetic energy is reduced by the same amount.
Important concepts
External forces or energies, such as gravity or friction, cause kinetic energy to vary. You’re probably familiar with the law of conservation of energy. Energy is only converted from one form to another, according to the law of conservation.
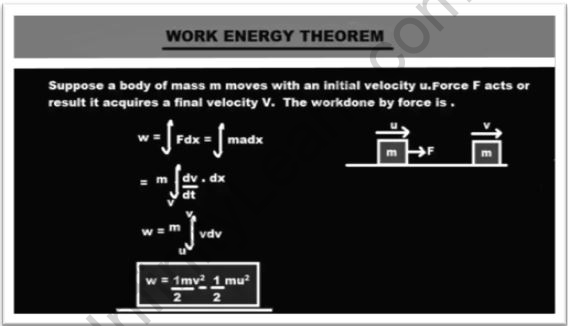
The Work-Energy Theorem states that,
Change (Difference) in Kinetic Energy = Work (performed by all types of energy or forces)
The formula for Work-Energy Theorem
Wnet = K−K0 =ΔK
Wnet is net-work and K is final kinetic energy and K0 is the initial kinetic energy, and lastly, ΔK is changing in kinetic energy Or
Wg + WN + Wf =Kf – Ki
Where Wg = work done by gravity
WN = work done by a reasonable force
Wf = work done by friction
Kf = final kinetic energy
Ki = initial kinetic energy
Use of the Work-Energy Theorem
The Work-Energy theorem’s application is that it is highly useful in assessing situations where a stiff body must move under many forces. Due to its rigid structure, a rigid body cannot store potential energy in its lattice and can only possess kinetic energy. The work done by any force that acts on a rigid body eventually equals the change in its kinetic energy, which is the foundation of the rigid body work-energy equation.
The Work-Energy Theorem’s Limitations
The rule was derived from Newton’s second law, and so it is applicable to particles. This rule applies to objects that are similar to particles. So, if all of the object particles act like particles, the entire object can be considered a particle.
The work-energy theorem is used to address a variety of problems, but it has the drawback of not providing entire information about the true cause of motion, which is the dynamics of Newton’s second law of motion, also known as the scalar version of Newton’s second law of motion. The direction of velocity is likewise not defined by the work-energy theorem.
The principle of work–energy
The work and kinetic energy concept (also known as the work-energy principle) asserts that the work performed by all forces acting on an object equals the change in the particle’s kinetic energy. In other words, the work W done on a particle by the resultant force equals the change in the particle’s kinetic energy Ek.
Newton’s second rule of motion and the resulting force on a particle are used to derive the work-energy principle. The instantaneous power added to the system is determined by computing the scalar product of the forces with the particle’s velocity.
The work-energy theorem has the following characteristics:
- There is no change in Kinetic energy when the particle’s usual speed is constant, and the work performed by the resultant force is zero.
- The Work-Energy Theorem states that if no exterior work is done, the Kinetic energy before and after a process must be equal.
- According to the work-energy theorem, a particle’s kinetic energy reduces by an amount equal to the amount of work it does.
Significance of work-energy theorem in the IIT JEE exam
The chapter on Work, Energy, and Power accounts for about 4% of the total number of questions addressed in the last 33 years. Work, Energy, Work-Energy Theorem, Power, Collisions are all significant sub-topics in Work, Energy, and Power. The most essential chapter in modern physics is awarded a weightage of 13.3 percent, with the remaining chapters receiving 3.3 percent and 6.6 percent respectively.
FAQs
Q. How do you tackle challenges involving the work-energy theorem?
Ans: The following steps should be taken into account:
Step 1: Draw the object’s FBD to determine the forces that are acting on it.
Step 2: Determine the kinetic energy of the starting and end states.
Step 3: Using the theorem to equivalence the values.
The work-energy theorem has the advantage that if an item moves from point A to point B, the work done on it can be calculated by integrating the area that is applied as a force and multiplying it by the work done. Knowing the effort done allows you to quickly determine the amount of energy used to move an object from one location to another. When there are no losses, this condition will be confirmed correctly. As a result, by factorizing the flaws, energy can be saved. What advantages does the work-energy theorem have?
Q. What are the steps to solving work-energy theorem problems?
Ans: The following are the steps to addressing questions involving the work-energy theorem:
- To begin, create a free-body diagram of the object to identify the forces acting on it.
- After that, calculate the initial and end kinetic energy.
- The values are then equated using the theorem.









