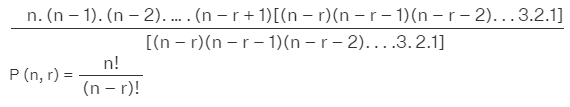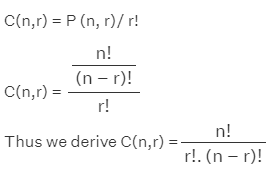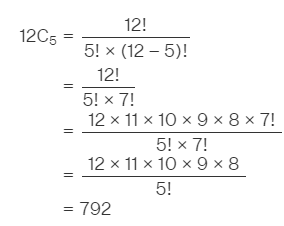Table of Contents
It is the way to represent a group of objects by selecting in a set and forming subsets. It defines the various ways to arrange a certain group of data. When we select the data or objects from a certain group, it is said to be permutations, whereas the order in which they are represented is called combination. Both concepts are very important in Mathematics. In order to understand permutation and combination, the concept of factorial has to be recalled. The product of the first n natural numbers is n! The number of ways of arranging n unlike objects is n!.
Permutation and combination are explained here in detail, along with the difference between them. We will discuss both the topics here with their formulas, real-life examples and solved questions.
Definition of permutation and combination:-
Permutation:- A permutation is an arrangement in a definite order of a number of objects taken some or all at a time. Let us take 10 numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. The number of different 4-digit-PIN which can be formed using these 10 numbers is 5040. P(10,4) = 5040. This is a simple example of permutation. The permutations of 4 numbers taken from 10 numbers equal to the factorial of 10 divided by the factorial of the difference of 10 and 4. The permutations is easily calculated using this formula.
Combination:- The combination is a way of selecting items from a collection, such that the order of selection does not matter. In smaller cases, it is possible to count the number of combinations. Combination refers to the combination of n things taken k at a time without repetition. To refer to combinations in which repetition is allowed, the terms k-selection or k-combination with repetition are often used. Permutation and Combination Class 11 is one of the important topics which helps in scoring well in Board Exams.
Permutation and Combination Formula:- The counting situation is analyzed to determine whether to employ permutations or combinations. Accordingly, the permutation and combination formulas are applied.
here we will discuss different types of a combination formula
Formula 1: Factorial of a natural number n.
n! = 1 × 2 × 3 × 4 × …….× n
Formula 2: The number of distinct permutations of r objects which can be made from n distinct objects is
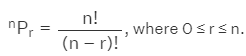
, where 0 ≤ r ≤ n.
Formula 3: The number of permutations of n different things, taken r at a time, where repetition is allowed, is nr.
Formula 4: The number of permutations of n objects taken all at a time, where objects are of the first kind, 
objects are of the second kind, …, 
objects are of the kth kind and the rest if any, and if all are different is
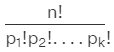
Formula 5: The number of combinations of n different objects taken r at a time is given by
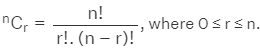, where 0 ≤ r ≤ n.
This formula is sometimes also called as ncr formula.
Formula 6: The relationship between permutation and combination for r things taken from n things.
Derivation of Permutation and Combination Formula:-
- The permutations formula:- The total number of permutations of a set of n objects taken r at a time P(n,r) = n!/(n-r)!, where [n>= r]
The combination formula:- The total number of combinations of a set of n objects taken r at a time C(n,r) = n!/[r !(n-r)!], where [n>= r]
Derivation of Permutations Formula:-
Since a permutation involves selecting r distinct items without replacement from n items and order is important, by the fundamental counting principle, we have
P (n, r) = n . (n-1) . (n-2) . (n-3)…… (n-(r-1)) ways.
This can be written as:
P (n, r) = n.(n-1).(n-2). (n-3) …. (n-r+1)—————(1)
Multiplying and Dividing (1) by (n-r) (n-r-1) (n-r-2)……….. 3. 2. 1, we get
P (n, r) =
Derivation of Combinations Formula:-
Since combinations involve choosing r objects out of n objects where the order doesn’t matter, we can determine as that:
C(n,r) = the number of permutations /number of ways to arrange objects. [Since by the fundamental counting principle, we know that the number of ways to arrange r objects in r ways = r!]
Difference between Permutation and Combination:-
The difference between Permutation and Combination can be understood through the following points.
- Permutations are used when order/sequence of arrangement is needed. Combinations are used when only the number of possible groups are to be found, and the order/sequence of arrangements is not needed.
- Permutations are used for things of a different kind. Combinations are used for things of a similar kind.
- The permutation of two things from three given things a, b, c is ab, ba, bc, cb, ac, ca. The combination of two things from three given things a, b, c is ab, bc, ca
- For different possible arrangement of things nPr=n!/(n-r)!. For different possible selection of things nCr =n!/r!(n-r)!
- For a given set of n and r values, the permutation answer is larger than the combination answer.
Example 1: Patricia has to choose 5 marbles from 12 marbles. In how many ways can she choose them?
Solution:
Patricia has to choose 5 out of 12 marbles. The order doesn’t matter here.
Thus combinations are used here. she can choose it in 12C ways.
Therefore she can choose 792 ways.
FAQ’s
What are Permutation and Combination?
Permutation and combination are the principles of counting used in various situations. Permutations are the form of counting used in the arrangement of r distinct objects out of n distinct objects. Combinations are the form of counting used in the selection of r different objects taken from n different objects.
How do you find Factorial of a Number?
The factorial of a number is obtained by taking the product of all the numbers from 1 to n in sequence. Here we have n! = 1 × 2 × 3 × 4 × 5 × .......n. As an example let us find the value of 5! = 1 × 2 × 3 × 4 × 5 = 120. The formula of n! is used in the formulas of permutation and combination.
