Table of Contents
The NTA (National Testing Agency) will soon release the JEE Main Mathematics syllabus for 2024 online. You can access this syllabus through the information booklet. The syllabus will cover topics from both class 11 and 12 mathematics. It’s essential for candidates to review the JEE Main Maths syllabus PDF for 2024 to understand what topics they need to focus on for their exam preparation.
Mathematics is often considered a challenging and comprehensive subject, requiring special attention. To enhance your preparation, you can also refer to the previous year’s JEE Main question papers. The JEE Main 2024 syllabus will be accessible online, and it’s important to be familiar with the exam pattern as well.
When preparing for the exam, it’s crucial to stick to the official JEE Main Mathematics syllabus for 2024, as questions will be based on these topics. Mathematics involves calculations, so having an analytical approach to problem-solving is important. In previous years, questions have been drawn from topics like Differential Calculus, Integral Calculus, Binomial Theorem, Permutations and combinations, Coordinate Geometry, Vectors, 3D Geometry, and others.
We recommend covering the entire Mathematics syllabus for JEE Main 2024 and then practicing with JEE Main mock tests to gauge your level of preparation. Keep in mind that JEE Main 2024 is expected to be conducted in two sessions, one in January and another in April. For more detailed information on the Mathematics syllabus for JEE Main 2024, please refer to the article below.
JEE Main Mathematics Syllabus:
The syllabus for JEE Main Mathematics is divided into 16 units. Each unit contains sub-topics based on mathematical concepts. To ace the JEE Main exam, you must thoroughly prepare for all of these topics.
The mathematics section of the JEE Main exam evaluates your numerical problem-solving abilities. The syllabus for the JEE Main Mathematics section is provided below.
UNIT 1: Sets, Relations, and Functions
The representation of sets; The algebraic properties of union, intersection, and complement of sets; power set Relationships, types of relations, equivalence relations, functions; one-to-one, into and onto functions, function composition.
UNIT 2: Complex Numbers and Quadratic Equations
Complex numbers as ordered pairs of reals, complex number representation in the form a + ib, and complex number representation in a plane Argand diagram, algebra of complex numbers, modulus and argument (or amplitude) of a complex number, square root of a complex number, triangle inequality, quadratic equations in the real and complex number systems, and their solutions. The relationship between roots and coefficients, the nature of roots, and the formation of quadratic equations with given roots are all discussed.
UNIT 3: Matrices and Determinants
Matrices, matrices algebra, matrices types, determinants, and matrices of order two and three. Determinant properties, evaluation of determinants, and area of triangles using determinants. Test of consistency and solution of simultaneous linear equations in two or three variables using determinants and matrices, adjoint and evaluation of inverse of a square matrix using determinants and elementary transformations.
UNIT 4: Permutations and Combinations
The basic principle of counting, permutation as an arrangement and combination as selection, the meaning of P (n, r), and simple applications.
UNIT 5: Mathematical Induction
The principle of mathematical induction and its simple applications.
UNIT 6: Binomial Theorem and its Simple Applications
Binomial theorem for a positive integral index, general and middle terms, Binomial coefficient properties, and simple applications.
UNIT 7: Sequence and Series
Arithmetic and geometric progressions, arithmetic and geometric means between two the numbers provided. The relationship between A.M. and G.M. Add up to n special series terms: Sn1, Sn2, and Sn3. Geometric progression in arithmetic.
UNIT 8: Limit, Continuity and Differentiability
Real-valued functions include function algebra, polynomials, rational, trigonometric, logarithmic, and exponential functions, as well as inverse functions. Graphs of simple functions. Limits, continuity, and differentiation are all critical factors to consider. Differentiation of the sum, product, quotient of two functions, and difference. Differentiation of trigonometric, inverse trigonometric, logarithmic, exponential, composite, and implicit functions; derivatives of up to two orders. Mean Value Theorems of Rolle and Lagrange. Derivative applications include the rate of change of quantities, monotonic – increasing and decreasing functions, maxima, and minima of functions of one variable, tangents, and normals.
UNIT 9: Integral Calculus
As an antiderivative, integral. Integrals with algebraic, trigonometric, exponential, and logarithmic functions. Substitution, parts, and partial fractions are all methods of integrating. Trigonometric identities are used for integration. Simple integrals of the type are evaluated.
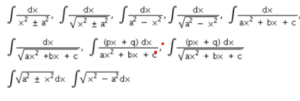
The limit of an integral is a sum. Calculus’s Fundamental Theorem. The characteristics of definite integrals. Determining the areas of regions bounded by simple curves in standard form using definite integrals.
UNIT 10: Differential Equations
Ordinary differential equations, their degree and order. Differential equations are created. Differential equation solution using the variable separation method, solution of homogeneous and linear differential equations of the type:
UNIT 11: Coordinate Geometry
Cartesian coordinate system in a plane, distance formula, section formula, locus and its equation, axes translation, slope of a line, parallel and perpendicular lines, intercepts of a line on the coordinate axes.
- Straight lines:
Equations of a line, angles between two lines, equations of internal, conditions for concurrence of three lines, intersection of lines, distance of a point from a line, and external bisectors of angles between two lines, centroid, orthocentre, and circumcentre of a triangle, equation of family of lines passing through the point of intersection of two lines.
- Circles, conic sections:
The standard form of a circle’s equation, the general form of a circle’s equation, its radius and center, the equation of a circle when the endpoints of a diameter are given, the points of intersection of a line and a circle with the center at the origin, the condition for a line to be tangent to a circle, and the equation of the tangent. Sections of cones, equations of conic sections (parabola, ellipse, and hyperbola) in standard forms, condition for y = mx + c to be a tangent and point (s) of tangency.
UNIT 12: Three-Dimensional Geometry
A point’s coordinates in space, the distance between two points, and the section formula. Angles between intersecting lines, direction ratios, and cosines are all examples of cosines. Skew lines are defined by the shortest distance between them and their equation. A plane in different forms and Equations of a line, the intersection of a plane and line, and coplanar lines.
UNIT 13: Vector Algebra
Vectors and scalars, addition of vectors, components of a vector in two dimensions and three-dimensional space, scalar and vector products, scalar and vector triple products.
UNIT 14: Statistics and Probability
- Measures of Dispersion: Calculate the mean, median, and mode of grouped and un-grouped data. Standard deviation, variance, and mean deviation for grouped and un-grouped data are computed.
- Probability: Probability of an event, probability addition and multiplication theorems, Baye’s theorem, probability distribution of a random variate, Bernoulli trials, and the Binomial distribution are all covered.
UNIT 15: Trigonometry
Identity and equations in trigonometry. Trigonometric functions are used to calculate angles. The properties of inverse trigonometric functions. Height and distance are both important considerations.
UNIT 16: Mathematical Reasoning
Logical operations, statements, and/or, implied by, implies, if, and only if. Tautology, converse, contradiction, recognize, and contra positive.
Frequently Asked Questions on JEE Main Mathematics Syllabus
What is the JEE Main Mathematics Syllabus for 2024?
The JEE Main Mathematics Syllabus for 2024 is divided into 16 units, covering topics from both class 11 and 12 mathematics. It includes topics such as sets, complex numbers, matrices, permutations, mathematical induction, binomial theorem, sequences, limits, calculus, differential equations, coordinate geometry, three-dimensional geometry, vector algebra, statistics, probability, trigonometry, and mathematical reasoning.
Where can I access the JEE Main Mathematics Syllabus PDF for 2024?
The JEE Main Mathematics Syllabus for 2024 can be accessed online through the official website of the National Testing Agency (NTA). You can also refer to the information booklet for detailed syllabus information.
How should I prepare for the JEE Main Mathematics exam?
To prepare for the JEE Main Mathematics exam, it's essential to thoroughly cover all the topics mentioned in the syllabus. You can start by understanding the fundamental concepts and then practise solving a variety of problems. Referring to previous year question papers and taking mock tests can help you gauge your preparation level. Additionally, having a strong analytical approach to problem-solving is crucial in mathematics.
Are there any specific topics that I should focus on for JEE Main 2024?
While all the topics in the JEE Main Mathematics syllabus are important, some frequently tested areas include calculus (both differential and integral), coordinate geometry, vectors, three-dimensional geometry, and algebraic concepts like complex numbers and matrices. However, it's advisable to cover the entire syllabus comprehensively.
When will JEE Main 2024 be conducted?
JEE Main 2024 is expected to be conducted in two sessions, one in January and another in April. It's essential to keep an eye on the official announcements and updates from the National Testing Agency for specific exam dates and other details








