Table of Contents
In solid-state physics, band theory is a theoretical model that describes the states of electrons in solid materials that can only have energy values within certain specific ranges. The behaviour of an electron (and thus its energy) in a solid is related to the behaviour of all other particles around it. This is in stark contrast to an electron’s behaviour in free space, where it can have any energy. Allowable bands are the ranges of electron energies in a solid. Certain ranges of energies between two such allowed bands are referred to as forbidden bands; that is, electrons within the solid are not permitted to have these energies. The band theory accounts for many of solids’ electrical and thermal properties and is the foundation of solid-state electronics technology. The discrete allowed energies—the energy levels—of single, isolated atoms are related to the band of energies permitted in a solid.
When atoms are combined to form a solid, the discrete energy levels are perturbed by quantum mechanical effects. The many electrons in the collection of individual atoms occupy a band of levels in the solid known as the valence band. Empty states in each atom also broaden into a band of usually empty levels known as the conduction band. Just as electrons at one energy level in an individual atom can transfer to another empty energy level, electrons in a solid can transfer from one energy level in a given band to another in the same band or another band, frequently crossing a forbidden energy gap in the process.
Overview
Studies of such energy changes in solids interacting with photons of light, energetic electrons, X-rays, and the like confirm the band theory’s general validity and provide detailed information about allowed and forbidden energies.
The band theory of Metals is based on the valence and conduction bands. It is also known as solid band theory or zone theory of solids. It defines conductors, semiconductors, and insulators in great detail.
Before you can understand band theory, you must first understand the following terms:
The valence band is made up of electron-containing valence shell orbitals. A sodium valence band, for example, is made up of 3s1 orbitals. Sodium has the electronic configuration 1s2, 2s2, 2p6, and 3s1. Metals conduct electricity due to the presence of valence electrons. The atomic orbitals of metals with the same energy combine to form molecular orbitals that are close in energy to each other, resulting in the formation of a band. If the bar is only partially filled or overlaps with another higher energy unoccupied conduction band, electrons can easily flow under an applied electric field, demonstrating high conductivity. According to band theory, atomic orbitals of the same symmetry found in all atoms of a metallic solid combine to form several energy bands, such as the 1S, 2S, 2P, 3S, and 3P bands.
There are a lot of molecular orbitals in these bands. Two electrons can exist in each molecular orbital. As a result, the inner bands of metals are filled bands, whereas the valence band is only partially filled.
In some cases, when the energy bandgap between the conduction and valence bands is large enough, electrons fail to jump from the valence band to the conduction band. They, like these compounds, have very little or no conductivity. For example, in glass, when the energy band gap between the conduction and valence bands is small, a few electrons may jump to the conduction band from the valence band, resulting in some conductivity. These substances are known as semiconductors—for example, Si and Ge (Silicon and Germanium, respectively).
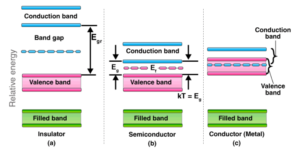
Band theory of metallic bonding
Metals have their valence band filled, and their conduction band is partially filled due to the lack of a bandgap. The theory predicts that metals will conduct (both heat and electricity) extremely well and is widely accepted. We know that molecular orbitals are formed by atomic orbitals overlapping. The molecular orbital approach is used in this model. For example, two molecular hydrogen molecules (H2) are formed by overlapping two hydrogen atoms. The energies of the two orbitals differ. One orbital will have a higher energy level, while the other will have a lower one. The orbital energies were represented by the energy level, the magnitude of which varied with the nuclear distance between the two atoms.
AB denotes the difference in energy between two molecular orbitals at equilibrium internuclear distance. If n number of atomic orbitals overlap, they will form n molecular orbitals. The atomic orbitals must have the same symmetry and associate with the same or similar amount of energy for overlapping to occur.
Molecular orbital band theory
In chemistry, molecular orbital theory (MO theory or MOT) uses quantum mechanics to describe the electronic structure of molecules. It was proposed in the early twentieth century. In molecular orbital theory, electrons in a molecule are not assigned to individual chemical bonds between atoms. Still, they are treated as moving under the influence of the atomic nuclei in the entire molecule. The spatial and energetic properties of electrons are described by quantum mechanics as molecular orbitals that surround two or more atoms in a molecule and contain valence electrons between atoms. MOT offers a global, delocalized view of chemical bonding.
According to MO theory, an electron in a molecule can be found anywhere in the molecule because quantum conditions allow electrons to travel under the influence of an arbitrarily large number of nuclei as long as they are in eigenstates permitted by certain quantum rules. Thus, electrons can transition to higher-energy molecular orbitals when excited with the appropriate amount of energy via high-frequency light or other means. For example, in the simple case of a diatomic hydrogen molecule, UV radiation can promote a single electron from a bonding orbital to an antibonding orbital. This promotion weakens the bond between the two hydrogen atoms and can result in photodissociation—breaking a chemical bond due to light.
Band theory explains the relationship between a metal’s valence electron configuration and the strength of metallic bonding. Because the valence electrons are not confined to a specific orbital, these atomic orbitals are close enough in energy that the derived bands overlap.
FAQ’s
What is the purpose of band theory?
The band theory of solids describes the quantum state that an electron acquires inside a metal solid. Every molecule has a unique energy level. Band theory adequately explains the behaviour of electrons within a molecule.
What exactly is conduction band theory?
When electrons are excited, they can jump into the conduction band, which is made up of electron orbitals. Electrons in these orbitals have enough energy to move freely in the material. This movement of electrons results in the generation of an electric current.
How does band theory explain lithium's metallic character?
Electrons can be fed into one end of a metal wire and removed from the other without affecting the metal's physical or chemical properties. Because there is virtually no overlap between two lithium atoms, the 1s core electrons remain unchanged.







