Center of Mass of a Two-Particle System

Introduction:

The center of mass of the system of a particle can be described as a point at which the whole mass of the body appears to be concentrated. In physics, the physics center of mass can be defined as the point at the center of the distribution of mass in space whereas in the weighted relative position of the distributed mass has a total sum of zero. Simply the center of mass is a position that is relative to an object. We can also say that it is the average position of all the parts of the system or it can be the mean location of a distribution of mass in any space. The center of mass is a point where force is usually applied which results in the linear acceleration without having any angular acceleration.

A brief outline of the topic:

The homogeneous bodies are the objects which have a uniformly distributed mass around the entire body. Some examples of homogeneous bodies are spheres, rings, etc. These rigid bodies are with a regular shape and for the calculation of the center of mass for these, we need to keep the symmetry between these particles. According to the symmetric considerations, we can presume that the center of mass for these regular bodies is present at their geometric centers.

A brief note of important concepts and laws:

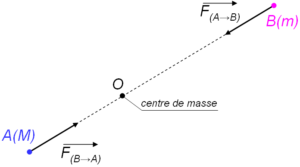
The center of mass for the system having two particles is given as:

For the system having two particles with equal masses, the center of mass is the point that is present exactly in the middle of both these particles. Suppose two particles with masses m1 and m2 respectively are present on the x-axis. The distance of both the particles from the center O is d1 and d2 respectively. The center of mass of this system having two particles is at point C present at a distance D from point O.

Therefore in this system having two particles D can be written as follows:

D =m ₁ d ₁ + m ₂ d ₂ ⁄m 1 + m ₂

From the above equation of D we can take the mean mass of d1 and d2. Now, let us assume that the particles in the system have almost equal masses.

Therefore m ₁=m ₂ = m

D =( m d ₁ + m d ₂) ⁄ 2 m

=m (d ₁ + d ₂) ⁄ 2 m

= d 1 + d ₂ ⁄ 2

From the above-mentioned equation, we get that the center of mass of a system has two particles with equal masses. From the above-given equation, it is crystal clear that the center of mass of two particles is present in the middle of both particles.

The center of mass for n particles is given as follows:

According to the definition for the system having n particles the center of mass is given as follows:

D = (m ₁ d ₁ + m ₂ d ₂ + m ₃ d ₃ +…… m n d n) ⁄ (m ₁ + m ₂ + m ₃ +.. m n m)

D= ∑midi ⁄mi

In the above equation,

mi = The sum of the masses of the particles

Let’s see the center of mass for the three particles at different positions:

It is not compulsory that the system of particles gives information about the center of mass present on the same axis of a straight line. There may be some cases when particles are present on the different lines far away from each other. Because these particles are present not in a straight line therefore there must be more than two particles. Let’s take the case of three particles present on the different axes x and y.

Here the positions of the particles are as (d ₁,e ₁ ), (d ₂,e ₂) and (d ₃,e ₃) along with the x and y-axes. The center of mass for the systems having three particles is located at point D and E and is given as follows:

D = (m ₁ d ₁ + m ₂ d ₂ + m ₃ d ₃ ) ⁄ (m ₁ + m ₂ + m ₃ )

E = (m ₁ e ₁ + m ₂ e ₂ + m ₃ e ₃ ) ⁄ (m ₁ + m ₂ + m ₃ )

Now if the particles contains equal masses i.e. m ₁ = m ₂ = m ₃ = m

Therefore,

D = [m (d ₁ + d ₂ + d ₃ ) ] ⁄ 3 m

= d ₁ + d ₂ + d ₃ ⁄3

E = [m (e ₁ + e ₂ + e ₃ )] ⁄ 3 m

= (e ₁ + e ₂ + e ₃ ) 3

From the above-mentioned equations, we can conclude that for a system of three particles, the center of mass lies at the centroid of the triangle formed by these three particles.

There are two types of work that work in a system: External Force: The force that is applied to the system from the outside is called the external force. The external force is equal to the rate of change of the momentum of the system. According to Newton’s second law mathematically the total external force will be given as follows: F ext = d ⁄ d t (m 1 v 1+ m 2 v 2 ) Internal Force: This force on a particle is dependent on its physical properties. When the particle taken is more than one then the Coulomb force acts between them. The gravitational force acts between them when there is more than one tiny massive particle.

FAQs (Frequently Asked Questions):

Question: Give two characteristics of the Center of Mass?

Answer: The characteristics of the center of mass are as follows:

• The center of mass of any system of particles is dependent on the masses of the particles and their relative positions.
• The mass moment of the system of particles about the center of mass is always equal to zero.

Question: Write any one characteristic property of the Center of Gravity?

Answer: The main characteristic property of the center of gravity is that it is responsible to carry the entire mass of the body.

Question: How is the motion in a rigid body described?

Answer: In the rigid body motion all lines on a rigid body contain the same angular velocity as well as the same angular acceleration. The rigid motion is decomposed into the translation of an arbitrary point following a rotation about the point.

Question: What is meant by the term Linear Momentum?

Answer: The linear momentum of the vector quantity in classical physics is equal to the product of the mass and the velocity of the center of mass.