Table of Contents
One of the easiest approaches for determining the molecular weight of different compounds has been to use the colligative characteristics of the solution. Because the colligative characteristics of solutions are determined only by the number of solute molecules present, this approach is particularly useful for measuring the molar weights of complicated molecules, proteins, macromolecules, and polymers.
A known concentration of the drug is produced in a solvent with a given boiling point, freezing point, or vapour pressure. The property to be measured is chosen in such a manner that it is simple and straightforward to measure under the specified conditions and does not fluctuate significantly.
Molecular weight is often referred to as molecular mass. The total of the atomic masses of all the atoms in a molecule is the molecule’s molecular mass.
Types of Colligative Properties:
- osmotic pressure
- elevation in boiling point
- depression in freezing point.
Simply put, colligative qualities are determined by the number of solute particles and are unaffected by the identity of the solute particles. A solution with a given concentration of a chemical is treated in a solvent with known vapour pressure, freezing, or boiling point. The property to be measured is chosen in such a way that its measurements are easy and simple under certain conditions, and they do not vary appreciably.
- Elevation of Boiling Point
When a non-volatile solute is introduced to a pure solvent, its boiling point rises. This increase in boiling point is proportional to the solute concentration in the solution.
It’s mathematically represented as:
∆Tb = Kbm
Where,
∆Tb = the elevation in boiling point
Kb = Constant of Boiling Point Elevation
m = Solution’s molal concentration
Molality, as we know, refers to the number of moles of solute per kilogram of a solvent.
So, now let’s take solute’s weight as w2, which is having molar mass M2dissolved in the solvent of w1 grams. Then, molality can be expressed as:
m = moles of solute / mass of solvent in Kg = w2/M2w1/1000
⇒m=1000×w2 / w1×M2
The elevation of boiling point is given as:
∆Tb = Kb×1000×w2 / w1×M2
So, now if you rearrange the above equation, we will get:
⇒M2 = Kb × 1000 × w2 / w1 × ∆Tb
The relationship between colligative property and molecular weight, which is boiling point elevation, is given by the equation above.
- Depression of Freezing Point
Similar to the elevation of the boiling point, the depression of the freezing point is a colligative feature of solutions that provides a way for determining the molar masses of diverse compounds. We know that freezing point depression is provided as:
∆Tf =Kfm
Where, ∆Tf = depression of freezing point
Kf = Freezing Point Constant
m = molal concentration of the solution
From the above explanation, now, it’s known that molality is expressed as:
M = 1000×w2 / w1×M2
Thus,
The depression in Freezing point is expressed as:
∆Tf= Kf×1000×w2 / w1×M2
Now rearranging the above equation, we get:
=>M2= Kf×1000×w2 / w1×∆Tf
As a result, if we can calculate the freezing point depression of the solvent when the solute is introduced, we can calculate the molar mass of the solute using the preceding equation.
- Osmotic Pressure
The pressure needed to simply halt the passage of solvent molecules across a semi-permeable barrier from a dilute solution to a concentrated solution is known as osmotic pressure.
It is given mathematically as:
π=CRT
Where,
π =osmotic pressure
C= Molar concentration of the solution
R= Universal gas constant
T= Temperature
So, solutions’ molar concentration contains w2 gms of solute which has M2 molar mass and the net volume of solution is V liters, and can be represented as:
C = w2/M2 / V = W2 / V×M2
So, you can write the osmotic pressure now as:
Π = w2RT / M2 V
Rearranging the above-mentioned equation, we get the result,
M2 = w2RT / πV
Using the colligative features of the solution, we may compute the molecular weight of a chemical in this manner.
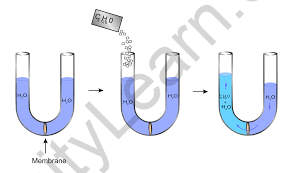
Using the colligative features of solutions, we may compute the molecular weight of the material. The three approaches outlined above give us alternatives based on the kind of material, the nature of the solvent, and the degree of precision necessary during measurement.
FAQs
What are the applications of colligative qualities in everyday life?
Colligative qualities are quite important in freezing point depression. Anti-freezers having a very low freezing point are commonly used in autos to aid in the operation of automotive engines. Because of the semi-permeability of the membrane, the process of osmosis is extremely beneficial in biological systems. The Osmosis technique is particularly advantageous in body systems since it aids in the absorption of nutrients in various body regions. Osmosis may also be used to remove waste items from the body.
What determines the Colligative properties?
Colligative qualities are those that are reliant on the concentration of solute ions in solute molecules. It is vital to note that colligative qualities are unaffected by the solute's identity. However, The colligative characteristics of solutions are those that are primarily determined by the concentration of solute ions or molecules. They are not determined by the solute's identification.
Explain how to calculate molar mass.
To calculate the molar mass of a solute in a solution, we must consider several factors, including the change in boiling point, which is the difference in temperature between the solution and the pure solvent, determining the molar concentration, which is determined by dividing the change in boiling point by the constant of boiling point elevation and calculating the molar mass from the mass of an unknown number of moles. A similar procedure may be used to calculate molar mass by reducing the freezing point and osmotic pressure. The molarity of the solution can be used to compute the moles of the unknown material. Calculate the product of the molality and the mass of the solvent to do this.





