Table of Contents
Introduction
We will discuss Vectors, equality of vectors, unit vectors, position vectors, zero vectors, and other related concepts in the simplest possible way. Mathematics is, without a doubt, the language of physics. It is easier to express, understand, and apply physical principles when one has a thorough understanding of mathematics. And we’ll be using algebra, trigonometry, and geometry regularly, as well as vector algebra, differential calculus, and integral calculus. Vectors, vector equality, unit vectors, and position vectors will all be covered in this lesson. Certain physical values can be completely stated numerically (with units specified) and added using basic algebraic concepts.
Mathematics certainly is the language of Physics. If one has a solid understanding of mathematics, it becomes easier to describe, understand, and apply physical principles. And we’ll be using algebra, trigonometry, and geometry, as well as vector algebra, differential calculus, and integral calculus, all the time. This topic will cover vectors, vector equality, unit vectors, and position vectors.
Certain physical quantities can be expressed completely by a numerical value (with units given) and added using standard algebraic principles. The mass of a system, for example, is described as 10 kg. When two bodies, one weighing 9 kg and the other weighing 11 kg, are combined to form a composite system, the total mass of the system is 11 kg + 9 kg = 20 kg. Scalars are such types of quantities, whereas those quantities that require direction along with magnitude are known as Vectors.
 Figure: One Image has a sense of direction other is directionless. From these two images, what conclusions can be drawn?
Figure: One Image has a sense of direction other is directionless. From these two images, what conclusions can be drawn?
Well, keep reading to know the answer!
Overview
Certain physical quantities require a numerical value (with units defined) as well as a spatial orientation to be fully described. A particle’s velocity is an example of this. A value like 5 m/s represents the magnitude of velocity, which informs us how rapidly a particle is moving. However, only when the direction of movement is defined does the description of velocity become complete. We can depict this velocity by drawing a line parallel to it and an arrow pointing in the direction of travel.
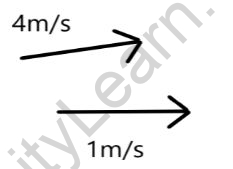
Figure shows, the magnitude as well as direction
In this part we shall learn the Equality, of Vectors and other related concepts mainly:
Scalar Quantity
Vector Quantity
Types of Vector
Unit Vector
Position Vector
Zero Vector
Scalar Quantity:
Scalar quantities are those that can only be described by a magnitude. They do not require a sense of direction. In other words, A scalar quantity is a type of quantity that can be completely described using their magnitude; they do not require direction.
For example, consider the terms “speed” and “mass.”
Vector Quantity:
In physics, a vector is a quantity with both magnitude and direction. It’s commonly depicted with an arrow that points in the same direction as the amount and has a length proportional to the quantity’s magnitude. For example, consider the terms Velocity, Force, Acceleration, etc.
Types of Vector
In Mathematics there are more than 10 types of Vectors, however, we will here discuss only a few which are important from the Vectors chapter’s point of view.
Unit Vector:
Unit vectors are vector quantities having a magnitude = 1 and are denoted by u=uu
Position Vector:
A position vector is simply a straight line attached to a body and the other end attached to a moving point. A position vector defines the relative location of a moving point to a body. The position vector will change length, direction, or both length and direction as the point moves.
Zero Vector:
A zero vector, abbreviated as 0, is a vector with length zero and zero components. It’s the additive identity of the vectors in an additive group.
When the magnitudes and directions of two vectors (indicating two values of the same physical quantity) are the same, they are said to be equal. As a result, a simultaneous translation of a vector does not affect it. This concept is known as the Equality of Vectors.
Example Problems
Question 1: Why do, Unit vectors have no unit?
Solution: A unit vector is defined as the vector divided by its magnitude. A unit vector has a magnitude of one unit because the numerator and denominator have the same numerical value. Similarly, because the numerator and denominator have the same unit, a unit vector is ‘unitless’ and thus dimensionless.
Importance of this chapter from JEE and NEET point of view
When there are quantities that must be described by both direction and magnitude, vectors are applied in many branches of physics. Vector values include displacement, velocity, acceleration, force, momentum, lift, thrust, friction, and weight (aerodynamic forces).
As an example of how vectors are used, the temperature of a particular medium is measured as a scalar quantity, but when the temperature of the medium decreases or increases, it is measured as a vector quantity.
Vectors and vector field notions are used to express electromagnetic laws and Maxwell’s equations.
You certainly cannot think of appearing in JEE, NEET, or even the boards if you don’t know the concepts of vectors.
The most fundamental concept in physics is vectors, which is also a high-scoring math chapter for the IIT JEE.
If you’re studying for the IIT-JEE or the NEET, you should get this chapter into your nerves.
Frequently Asked Questions
What is a Coplanar vector?
Coplanar Vectors are those that are in the same plane. These vectors are parallel to the same surface and are in the same plane. Three vectors are said to be coplanar when their scalar product equals zero.
What are Collinear vectors?
Collinear vectors are defined as two or more provided vectors that lie along the same line. Because two parallel vectors are pointing in the same or opposite direction, we can call them collinear vectors.
What is Like & Unlike vectors?
Like vectors are two vectors that have the same direction. On the other hand, unlike vectors are those that have the opposite direction concerning each other.







