Table of Contents
Temperature changes in thermal expansion can modify the form, volume, and area of matter. Temperature is defined as a monotonic function of a substance’s average molecular kinetic energy. When a substance is heated, its kinetic energy increases and a greater average spacing is maintained as the molecules begin to vibrate. The unusual temperature rises as a result of material contraction, and the effect is small. It usually occurs within a short temperature range, which is referred to as strain, and temperature changes are used to divide it. This process is known as the materials coefficient of thermal expansion, and it usually varies with temperature. In the field of physics, Thermal expansion is the change in length, width, height, or volume of any material as a result of a change in temperature. Because atoms are closely packed in solids, thermal expansion is particularly noticeable. Thermal expansion of solids is used in a variety of situations in everyday life.
Overview
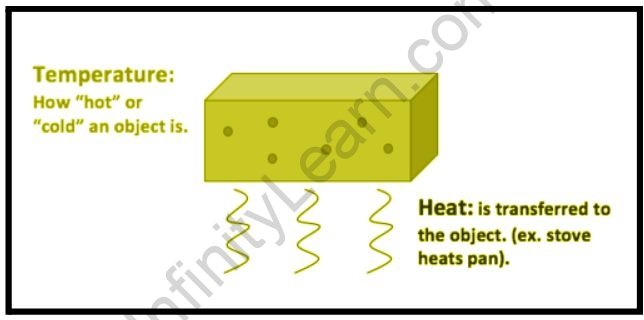
Heat is the total energy of the motion of a substance’s molecules, whereas temperature is the average energy of the motions of the molecules in the substance. The heat is affected by factors such as particle speed, particle size, and particle number, among others. The temperature, on the other hand, is unaffected by these variables. Let’s compare a tub of water to a cup of water, for example. The water in the tub and the water in the cup may be the same temperature, but due to the number of particles in the tub, the water in the tub has more thermal energy and thus more heat even though they are both the same temperature.
A temperature is a number that relates to the energy possessed by a substance’s molecules, which directly relates to the kinetic energy possessed by the substance’s particles. Temperature is measured in degrees Kelvin, the SI unit of measurement. As previously stated, the temperature is directly related to the kinetic energy of molecules; thus, doubling the temperature (in degrees Kelvin) of a substance doubles the average kinetic energy possessed by those molecules.
Thermal expansion
The tendency of matter to alter the shape, area, and volume in reaction to temperature variations is known as thermal expansion. Temperature is a monotonic function of a substance’s average molecular kinetic energy. The kinetic energy of a substance’s molecules increases when it is heated. As a result, the molecules begin to vibrate/move more and typically maintain a greater average separation. Materials that contract as the temperature rises are unusual; this effect is limited in size and occurs only within specific temperature ranges. The relative expansion (also known as strain) divided by the temperature change is known as the material’s coefficient of thermal expansion, and it varies with temperature.
There are three types of thermal expansion:
Linear thermal expansion
Areal thermal expansion
Volume thermal expansion
The coefficient of linear thermal expansion is defined as the relative expansion of the material divided by the change in temperature. In general, the coefficient of linear thermal expansion varies with temperature.
Linear expansion
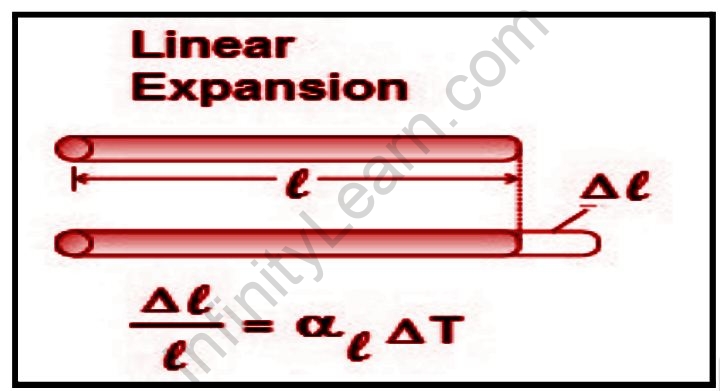
When a body is heated, its length expands proportionally to its original length or the change in temperature in the body. When calculating thermal expansion, it is necessary to take into account whether the body is free to expand or constrained to expand. If the body is free to expand, the expansion or strain caused by a temperature increase can be easily calculated by applying the applicable coefficient of Thermal Expansion. If the body is constrained in such a way that it cannot expand, then a change in temperature will cause (or change) internal stress. This stress can be calculated by taking into account the strain that would occur if the body were free to expand and the stress required to reduce that strain to zero, as described by the stress/strain relationship characterized by the elastic or Young’s modulus. Because external ambient pressure does not usually have a significant effect on the size of an object in the special case of solid materials, it is not usually necessary to consider the effect of pressure changes.
Linear expansion denotes a change in one dimension (length) rather than a change in volume (volumetric expansion). To a first approximation, the change in length measurements caused by thermal expansion is related to temperature change by a linear thermal expansion coefficient (CLTE). It is the fractional change in length per degree change in temperature. Assuming that pressure has no effect, we can write:
ΑL=dL/LdT
where L is a specific length measurement and dL/dT is the rate of change of that linear dimension per unit change in temperature.
The linear dimension change can be estimated to be:
∆L/L=ΑL∆T
This estimation works well as long as the linear-expansion coefficient does not change significantly with temperature change ∆T and the fractional change in length is small ∆L/L«1. If either of these conditions is not met, the exact differential equation must be integrated.
Area expansion
Area Expansion is defined as an increase in the area caused by an increase in temperature.
In the case of area expansion, there is an increase in both length and width.
As we can see from the images above, the area of the cube has increased from A to A+∆A.
Mathematically, this can be written as:
∆A/A=Aa∆T
Where Aa denotes the coefficient of area expansion.
The coefficient of area expansion is defined as the degree of area expansion divided by the temperature change.
This means that as the temperature rises, the area of an object expands.
It is denoted by the symbol Aa
It is a property of the substance that varies with temperature.
The area thermal expansion coefficient relates a change in the area dimensions of a material to a change in temperature. It is the fractional change in area per degree change in temperature. Ignoring the pressure, we could write:
Aa =dA/AdT
Where A represents an area of interest on the object and dA/dT represents the rate of change of that area per unit change in temperature.
The change in the area can be calculated as follows:
Aa/A=Aa∆T
This equation works well as long as the area expansion coefficient does not change significantly with temperature T and the fractional change in area is small A/A«1. If either of these conditions is not met, the equation must be solved.
Volume expansion
It is defined as volume expansion caused by an increase in temperature. This indicates that the length, width, and height of a substance have increased.
As we can see from the images above, the volume of the cube has been increased from V to V+ΔV, as have the length, width, and height. The expansion of volume is a result of an increase in temperature. Mathematically, this can be written as:
ΔV/V=Av ∆T
The coefficient of volume is defined as the degree of volume expansion divided by the temperature change.
It is represented by the letter Av
It is a property of the substance.
It varies depending on the temperature.
If a graph is drawn between v and temperature, it changes linearly at first, then non-linearly at higher temperatures, and finally becomes constant.
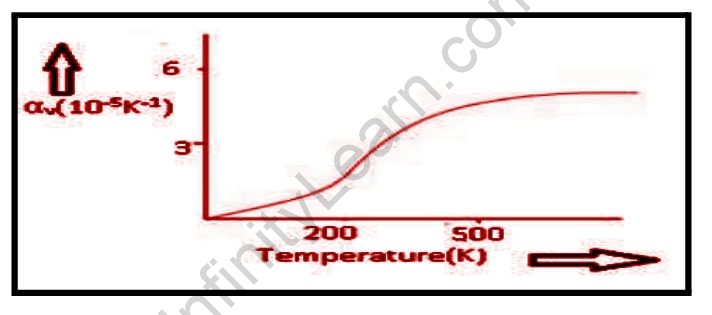
We can ignore the effects of pressure on a solid and calculate the volumetric (or cubical) thermal expansion coefficient:
Av=dV/VdT
where V is the volume of the material and dV/dT is the rate of change of that volume with temperature dV/dT is the rate of change of that volume with temperature
This means that a material’s volume changes by a fixed fractional amount.
When the temperature is raised by 50 K, a steel block with a volume of 1 cubic metre may expand to 1.002 cubic metres. This represents a 0.2 percent increase. If we had a block of steel with a volume of 2 cubic metres, it would expand to 2.004 cubic metres under the same conditions, a 0.2 percent increase. For 50 K, the volumetric expansion coefficient would be 0.2 percent or 0.004% K-1.
Frequently Asked Questions
What is thermal expansion?
Thermal expansion is the process by which an object or body expands when heated.
Thermal expansion effects which properties of matter?
Thermal expansion has an impact on the body's shape, volume, area, and density.
What is the coefficient of linear thermal expansion?
The coefficient of linear thermal expansion is defined as the relative expansion of the material divided by the change in temperature.








