Table of Contents
Introduction
The uncertainty principle (also known as Heisenberg’s uncertainty principle) in quantum mechanics is any of a number of mathematical inequalities that assert a fundamental limit to the accuracy with which from initial conditions, certain pairs of physical quantities of a particle, such as position, x, and momentum, p, can be predicted. Because the mathematical framework of quantum physics does not support the notion of simultaneously well-defined conjugate attributes stated by a single value, the uncertainty principle limits the extent to which such conjugate properties retain their approximate meaning.
The uncertainty principle implies that, even if all initial conditions are specified, it is generally not possible to predict the value of a quantity with arbitrary certainty. The uncertainty principle, first proposed by German physicist Werner Heisenberg in 1927, states that the more precisely a particle’s position is determined, the less precisely its momentum can be predicted from initial conditions, and vice versa.
Heisenberg concludes in his published 1927 paper that the uncertainty principle was originally ∆p∆q~h Earle Hesse Kennard later that year and Hermann Weyl in 1928 derived the formal inequality relating the positional standard deviation x and the momentum standard deviation _p:
σx σp=h/2
where is the Planck constant reduced, and h/(2π)
Because the uncertainty principle is such a fundamental result in quantum mechanics, typical quantum mechanics experiments routinely observe aspects of it. Certain experiments, on the other hand, may purposefully test a specific form of the uncertainty principle as part of their main research program. These include tests of number–phase uncertainty relations in superconducting or quantum optics systems, for example. One application that relies on the uncertainty principle for operation is extremely low-noise technology, such as that required in gravitational-wave interferometers.
The uncertainty principle of Heisenberg limits the accuracy of simultaneous measurement of position and momentum. The more precise our position measurement, the less precise our momentum measurement, and vice versa. The quantum system is the physical source of the Heisenberg uncertainty principle. Position determination by performing a measurement on the system disturbs it enough to make q determination imprecise, and vice versa. We’ll go over the principle in more detail later.
Overview
It is impossible to precisely measure or calculate an object’s position and momentum, according to Heisenberg’s uncertainty principle. This principle is based on matter’s wave-particle duality. Although Heisenberg’s uncertainty principle can be ignored in the macroscopic world (uncertainties in the position and velocity of objects with relatively large masses are negligible), it is extremely important in the quantum world.
Because atoms and subatomic particles have such small masses, any improvement in the precision of their positions will be accompanied by an increase in the uncertainty associated with their velocities. Heisenberg’s uncertainty principle is a fundamental theory in quantum mechanics that explains why it is impossible to measure more than one quantum variable at the same time. Another implication of the uncertainty principle is that it is impossible to precisely measure a system’s energy in a finite amount of time. The Heisenberg uncertainty principle is at the heart of quantum mechanics. Simply put, the principle states that there is a fundamental limit to what a quantum system can be known about. For instance, the more precisely one knows a particle’s position, the less precisely one can know its momentum and vice versa.
State Heisenberg uncertainty principle
The Heisenberg uncertainty principle states that it is impossible to precisely measure or calculate an object’s position and momentum. This principle is based on matter’s wave-particle duality. Another implication of this principle is that accurately measuring the energy of a system in a finite amount of time is impossible. Heisenberg’s uncertainty principle is a fundamental theory in quantum mechanics that explains why it is impossible to measure more than one quantum variable at the same time. This principle states that measuring an object’s position and momentum is impossible. Although Heisenberg’s uncertainty principle can be ignored in the macroscopic world, it is very important in the quantum world.
Heisenberg uncertainty principle formula
If ∆x is the error in position measurement and ∆p is the error in momentum measurement, then
∆x×∆p=h/4p
Because momentum, p = mv, Heisenberg’s uncertainty principle formula can be written as-
∆X×∆mv=h4p or ∆X×∆m×∆V=h/4p
Where ∆V is the measurement error in velocity and mass is assumed to be constant throughout the experiment,
∆X×∆V=h/4 pm
Accurate measurement of position or momentum implies greater uncertainty (error) in the measurement of the other quantity.
Using the Heisenberg principle on an electron in an atom’s orbit, with h=6.626×10-34J s and m=9.11×10-31Kg
If the electron’s position is accurately measured to its size (10-10m ), the error in measuring its velocity will be equal to or greater than 106m or 1000Km.
The Heisenberg principle only applies to dual-natured microscopic particles and not to a macroscopic particle with a very small wave nature.
Explain Heisenberg uncertainty principle
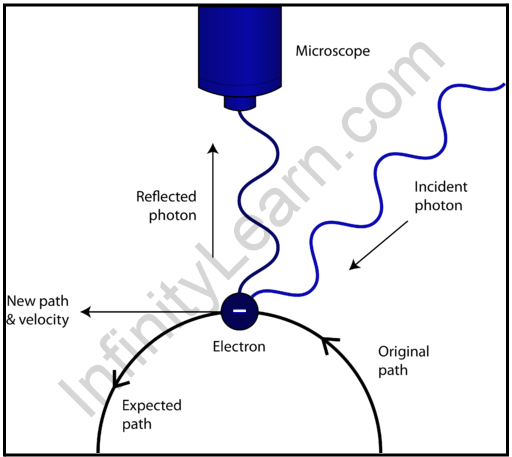
Electromagnetic radiations and microscopic matter waves have both a mass/momentum and a wave nature. The position and velocity/momentum of macroscopic matter waves can be precisely determined at the same time. For example, the location and speed of a moving car can be determined with minimal error at the same time. However, in the case of microscopic particles, it will be impossible to fix the particle’s position while also measuring its velocity/momentum. The mass of an electron in an atom is 9.91×10-31Kg. Such small particles are invisible to naked eyes.
A powerful light could collide with the electron, illuminating it. Illumination aids in the identification and measurement of the electron’s position. While assisting in the identification, the collision of the powerful light source increases the momentum of the electron and causes it to move away from its initial position. As a result, when the position was fixed, the particle’s velocity/momentum changed from its original value. As a result, when the position is exact, the error in measuring velocity or momentum occurs. Similarly, accurate momentum measurement will change the position.
As a result, at any point in time, only position or momentum can be accurately measured.
Simultaneous measurement of both will result in a position and momentum error. Heisenberg quantified the error in measuring both position and momentum simultaneously.
Also read: De Broglie’s Relationship
FAQs
In chemistry, what is the Heisenberg uncertainty principle?
According to Heisenberg's Uncertainty Principle, there is inherent uncertainty in the act of measuring a particle's variable. The principle, which is commonly applied to a particle's position and momentum, states that the more precisely the position is known, the more uncertain the momentum is, and vice versa.
What is the Heisenberg uncertainty principle?
According to Heisenberg's uncertainty principle, it is impossible to precisely measure or calculate an object's position and momentum. This principle is based on matter's wave-particle duality.
What is the formula for Heisenberg's principle?
The Heisenberg uncertainty principle is a mathematical lower bound on the product of uncertainties of two conjugate variables. The most well-known expression considers position and momentum to be conjugate variables xp=h2