Table of Contents
In an ideal gas, particles all travel at extremely high speeds, but not at the same rate. Although the RMS speed is a form of average, certain particles travel faster than others. Individual molecules in a gas move with random speeds in magnitude and direction, while a gas with numerous molecules has a deterministic distribution of molecular speeds. The Maxwell-Boltzmann distribution is named after its creators, who estimated it using kinetic theory, and it has subsequently been proven experimentally.
A brief outline
The velocity of gases is determined by their temperature and molecular masses, according to the Kinetic Theory of Gases. Random molecular motion has no average velocity. The velocity of the gas is found to be related to its temperature and inversely proportional to its molecular mass. When the temperature of the gas is raised, the velocity of the gas also rises, and the root means square velocity rises as well. A plot of a molecule’s percentage and velocity/speed at a given temperature is known as the Maxwell distribution curve. The number of molecules for that particular speed will be determined by the area under the curve. The peak will be pushed to the right when the gas is heated.
Important concepts
The formula for Molecular Speed
Gas particles are in constant motion and display perfectly elastic collisions, according to the Kinetic Molecular Theory of Gases. Gas particles are found in a permanent state of random motion, and until they hit another particle, they always proceed in a straight line. It also explains why a bunch of gas particles’ average kinetic energy is proportional to temperature.
The speed linked with a collection of molecules can be found in an ideal gas state.
KE=1/2mv2
The root-mean-square speed or molecular speed calculates the average speed of particles in gas and is written by
V = √3RT/m
Where:
V is the molecular speed of the particle
T is the temperature in Kelvin
M is the molar mass of the compound
R is the Ideal gas constant (8.314 kg×m2/s2×mol×K)
To understand the origins of ideal gas laws, one must first understand the kinetic molecular theory of gases.
- Gaseous particles, according to the kinetic molecular theory, are in a state of constant random motion; single particles travel at varying speeds, clashing and changing directions constantly.
- The most likely speed is the one that indicates the gas’s maximum molecules moving at the same time. The largest value on Maxwell’s distribution plot represents the most likely speed.
- The average speed is calculated by multiplying the sum of all the molecules’ speeds by the different molecules.
- The square root of the average velocity-squared of molecules in a gas is used to calculate the root-mean-square speed of particles in a gas.
Maxwell distribution of molecular speed
The Maxwell–Boltzmann distribution is derived from the kinetic theory of gases, which simplifies many fundamental gaseous phenomena such as pressure and diffusion. The Maxwell–Boltzmann distribution is fundamentally applicable to particle velocities in three dimensions, but it turns out to be dependent only on the particles’ speed (velocity magnitude). A particle speed probability distribution shows which speeds are much more likely: a particle would have a speed chosen at random from the distribution, and will be more likely to be in one range than another.
The classical ideal gas, which is an idealization of real gases, is covered by the kinetic theory of gases. There are a variety of phenomena in real gases that might cause their speed distribution to diverge from the Maxwell–Boltzmann form. Rarefied gases, on either hand, behave extremely nearly like an ideal gas at ordinary temperatures, and the Maxwell speed distribution is an effective approximation for such gases. Particle distributions in ideal plasmas, which are ionized gases with a sufficiently low density, are typically partially or totally Maxwellian.
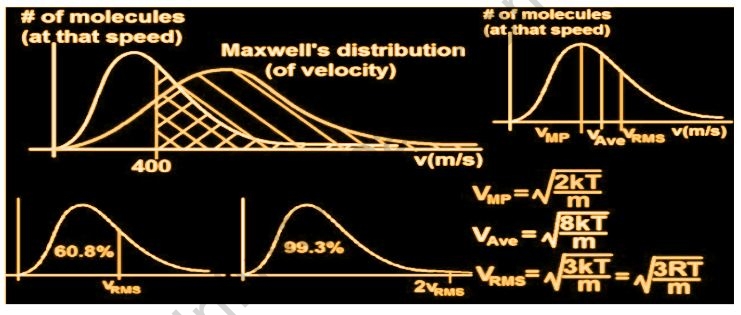
The air molecules that surround us do not all move at the same rate. Some air molecules move at a quicker rate, while others move at a slower rate or do not move at all. As a result, rather than asking about the speed of a single gas molecule, we ask about the speed distribution throughout a gas at a given temperature. James Maxwell and Ludwig Boltzmann devised a hypothesis to explain how the speeds of molecules in an ideal gas are dispersed.
Significance of molecular speed in NEET exam
This article on atomic speed gives complete data on the Maxwell appropriation of sub-atomic speed. Analyze the definite notes mindfully to guarantee that you comprehend this subject since it will assist you with planning for the following NEET test. You can likewise write down a few brief notes on the atomic speed to reference during the test.
The NEET subjects are intended to address and explain the most widely recognized inquiries on the test. These can be communicated in straightforward words with the assistance of notes from skilled analysts in the field, which are posted on the Infinity Learn online stage. Various decision questions are not difficult to rehearse assuming understudies have a decent comprehension of the subjects introduced all through the program.
Also read: Types of Bonding
Frequently Asked Questions
What is Boltzmann's Distribution Law, and how does it work?
Boltzmann's distribution law seems to be a probability measure that expresses the probability of a system being in a given state as a function of its energy and temperature T.
When the temperature rises, what occurs to the Maxwell distribution curve?
As the temperature rises, the entire distribution curve shifts to the right. The temperature has an influence on the Maxwell-Boltzmann distribution. The molecules have less energy at lower temperatures. As a result, the molecule's speeds are slower, and the distribution's range is narrower. The pattern flattens out as the temperature of the molecules rises. The molecules are travelling quicker because they have more energy at a higher temperature.








