Table of Contents
Introduction:
A solid is defined by its size and shape. A force is necessary to change (or deform) the shape or size of a body. When you gently pull the ends of a helical spring, the length of the spring rises somewhat. When you remove the spring’s ends, it returns to its natural size and shape.
Elasticity is a property of a body in which it tends to restore its original shape and size when the applied force is removed, and elastic deformation is the deformation produced by this property. When you apply force to a lump of putty or mud, however, it has little chance of regaining its original shape, and it becomes permanently distorted.
These substances are referred to as plastic, and their property is referred to as plasticity. Putty and mud are plastics that come close to being ideal.
In engineering design, the elastic behavior of materials is critical. For example, when designing a building, understanding the elastic qualities of materials like steel and concrete is critical. The same may be said for bridges, autos, ropeways, and other structures.
In this article, we will learn about Hooke’s law, Hooke’s which plays a crucial role in understanding the chapter Mechanical Properties of Solids. But before starting Hooke’s law, let us learn about Strain and Stress
Stress and Strain:
An object in static equilibrium is deformed to varying degrees by forces applied while it is still in equilibrium. The degree of the deformation depends on the material of the object and the size of the deforming force. Many materials display deformations that are invisible to the naked eye but exist nonetheless. The body develops a restoring force after experiencing a deforming force. Restorative forces are exerted in the opposite direction from the applied forces but have the same magnitude.
Restoring forces per unit area is what we call stress.
Then Magnitude of stress can be written as
Stress=F /A
SI unit of stress is Nm-2
When a solid is subjected to an external force, it can change its dimensions in three ways. Two equal forces applied normally to the cross-sectional area of a cylinder can stretch it.
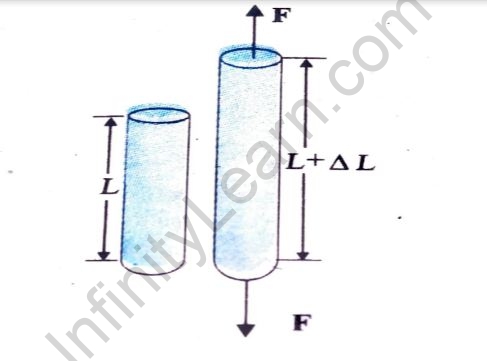
Tensile stress is the restoring force per unit area in this circumstance.
The restoring force per unit area is known as compressive stress when the cylinder is compressed under the action of applied forces.
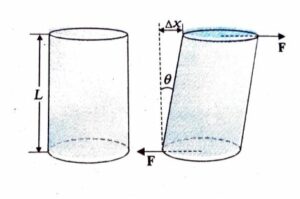
Shearing Stress on Cylinder
Longitudinal stress is another name for tensile or compressive stress. There is a variation in the length of the cylinder in both circumstances. Longitudinal strain is defined as the difference between the length and the initial length of the body.
Longitudinal strain =Δ L /L
There is the relative displacement between the opposite faces of the cylinder when two equal and opposite deforming forces are applied parallel to the cross-sectional area of the cylinder. Tangential or shearing stress is the restoring force per unit area created as a result of the applied tangential force.
Hooke’s Law:
Hooke’s law definition:
Hooke’s law was developed by the English scientist Robert Hooke in 1660, which asserts that the displacement or magnitude of deformation is directly proportional to the deforming force or load for relatively minor deformations of an object.
The stress in a body is proportional to the associated strain if the deformation is small.
Hooke’s law is the name given to this fact. When a rod is stretched by equal and opposite forces F, a tensile stress F/A is created in the rod, where A is the cross-sectional area. The rod’s length increases from L to L+ΔL, which is its natural value. Whereas L/ Δ L is the tensile strain.
By Hooke’s law, for small deformations,
Tensile stress / Tensile strain=Y
The ratio of tensile stress over tensile strain is called Young modulus for the material.
Further, Y can be written as
Hook Y=(F/A)/ Δ Ll
=(FL )/ AΔL
Example: A 4 kg load is suspended from a ceiling through an iron wire of length 20 meter and radius 2.0 mm. The change in length is 0.031 mm after the equilibrium is established. Find Young modulus of steel.
Solution:
Longitudinal stress = (4 .0 kg)(3.1?ms-2? )/ (2.010-3 m)2
= 3. 1 1 0 6 N m s-2
Longitudinal strain =0.3110-3 / 2.0 m
=0.015510-3
Therefore,
Y=3 . 1 1 06 N m s-2 / 0.015510-3
=2.0 1 0 1 1 N m-2
In this article we learnt about the Hooke’s law which is defined as a law of elasticity developed by the English scientist Robert Hooke in 1660, which asserts that the displacement or magnitude of a deformation is directly proportional to the deforming force or load for relatively minor deformations of an object. When the load is removed under these conditions, the item returns to its original shape and dimensions. The fact that minor displacements of their constituent molecules, atoms, or ions from normal locations are proportional to the force that generates the displacement explains the elastic behavior of solids according to Hooke’s equation. That’s it for this segment, further we will also cover other topics as well so stay tuned! I hope you would find this article as both informative as well as fun to read.
Also read: Young’s Modulus
Frequently Asked Questions FAQ’s:
Question 1: What is Bulk Modulus?
Answer: The elastic properties of a solid or fluid when it is under pressure on all surfaces are described by the bulk modulus, a numerical constant. The bulk modulus, also known as incompressibility, is a measurement of a substance’s ability to sustain changes in volume when compressed on all sides.
Question 2: What is the significance of bulk modulus?
Answer: The compressibility of a fluid is measured by its bulk modulus. With many hydraulic systems currently operating at pressures of 5000 psi and greater, disregarding bulk modulus might cause a system’s response time to be compromised. Rather than compressing the fluid, applied pressure should affect the system’s activity directly.
Question 3:What happens if you let go of the stretched rubber band?
Answer: The potential energy in the rubber band is immediately converted to kinetic (motion) energy when it is released.
Question 4: Does stress depend on Young’s Modulus?
Answer: In the elastic domain, stress is independent of Young’s modulus. Within the elastic limit, Hooke’s law states that stress is directly proportional to strain. Because a larger Young’s modulus reduces the strain caused in the material, the stress remains relatively constant.





