Table of Contents
The terms speed and speed provide us with a thought of how quickly or slow an article is moving. Regularly, we run over circumstances where we want to distinguish which of the at least two items is moving quicker. One can undoubtedly tell the quicker of the two assuming they are moving in a similar bearing on a similar street. In any case, in the event that their bearing of movement is the other way, it is hard to decide the quickest.
This is where speed becomes useful. As per the speed meaning, it tends to be characterized as the pace of progress of the item’s situation as for an edge of reference and time. It may sound convoluted, yet speed is fundamentally speeding in a particular course. It is a vector amount, and that implies we want both size (speed) and heading to characterize speed.
The amount that lets us know how quickly the item is moving anyplace along its way is the prompt speed, for the most part called essentially speed. It is the normal speed between two focuses on the way in the cutoff that the time (and hence the relocation) between the two focuses approaches zero. To outline this thought numerically, we want to communicate position x as a consistent capacity of t signified by x(t). The articulation for the normal speed between two focuses utilizing this documentation is
v = x(t2 ) – x (t1)/ t2 – t1
We characterise quick speed since there are applications where we need to know what the speed of an article is at some moment (as you call attention to this is to some degree helpless phrasing since speed indicates the difference ready throughout a period span; however it seems as though you have a grip of what we truly mean by immediate, so I will utilise that term here). For instance, the speedometer in your vehicle lets you know your quick speed while driving. Or on the other hand, to know the force of each article just before a crash, we would take a gander at the quick speed.
Unit of Instantaneous Velocity
The SI unit of instantaneous velocity is m/s. This is a vector quantity. By taking the slope of the distance-time graph or x-t graph, it can also be determined.
Formula for Instantaneous velocity
To find the instantaneous velocity at any position, we let t1=t and t2 = t+ Δt. After inserting these expressions into the equation for the average velocity and taking the limit as Δt ⟶0, we find the expression for the instantaneous velocity:
V(t) = limΔt ⟶0 x(t + Δt ) – x(t) / Δt
= dx(t)/dt
If the elapsed time approaches zero, the instantaneous velocity of an object is the limit of the average velocity or the derivative of x with respect to t:
V(t)= dx(t)/dt
Graphical Representation
Like normal speed, the momentary speed is a vector with an element of length for each time. The momentary speed at a particular time point t0 is the pace of progress of the position work, which is the incline of the position work x(t) at t0.
The chart shows how the normal speed between twice moves toward the momentary speed at t0. The quick speed is demonstrated at time t0, which turns out to be at the limit of the position work. The incline of the position diagram is zero now, and in this manner, the prompt speed is zero. At different times t1,t2, etc., the momentary speed isn’t zero in light of the fact that the slant of the position chart would be positive or negative.
On the off chance that the position work had a base, the slant of the position chart would likewise be zero, giving a momentary speed of no there also. In this manner, the zeros of the speed work give the base and limit of the position work.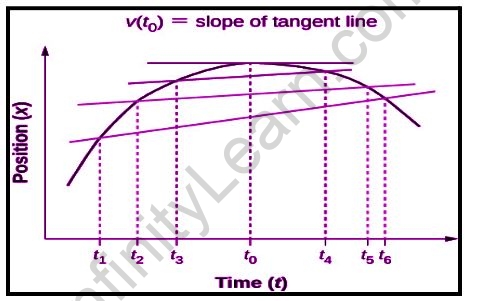
A graph showing position versus time shows instantaneous velocity as the slope of the tangent line. The average velocities v = xf – xi / tf – ti between times Δt= t6 – t1 and Δt= t5 – t2 Δt= t4 – t3 are shown.When Δt⟶ 0, the average velocity approaches the instantaneous velocity at t = t0
Instantaneous Velocity Example
Example 1
The particle’s displacement varies with time and is given as (6t2 + 2t + 4) m, the instantaneous velocity can be found out at any given time by:Answer:
s = (6t2 + 2t + 4)
Velocity (v) = ds/dt = d(6t2 + 2t + 4)/dt
=12t + 2
In order to find out the instantaneous velocity at t = 5 sec, we would put t in the expression of velocity obtained.
Instantaneous velocity at t = 5 sec = (12×5 + 2) = 62 m/sLet us now calculate the average velocity over 5 seconds.
Displacement = (6×52 + 2×5 + 4) = 164 m
Average velocity= 164/5
= 32.8 m/s
Example 2
Find out the Instantaneous Velocity of a particle traveling along a straight line for time 3 seconds, with a position function x defined as 5² + 2t + 4?Answer:As given in the function,x = 5t² + 2t + 4In order to compute Instantaneous Velocity for the given function, we differentiate the function with respect to t:Instantaneous = d( 5t² + 2t + 4)/dt = 10t + 2Putting value of t =3 , we get instantaneous velocity as
Instantaneous = 10 x 3 +2
= 32 m/s
Instantaneous Velocity FAQs
Is instantaneous velocity a scalar or vector?
Instantaneous velocity is a vector quantity.
If the object has an instantaneous velocity of 40 miles per hour. What is its instantaneous speed?
The object's instantaneous speed is 40 miles per hour.
How are instantaneous velocity and instantaneous speed related?
A speed is an indication of how fast the speed is at its actual instant.
What is a real-life example of instantaneous speed?
The instantaneous speed of an object can also be defined as a short distance travelled by it divided by the corresponding time taken. An object's instantaneous speed can change with every moment. Speedometers in cars, for instance, display the current speed of the vehicle on an instantaneous basis.





