Important Topic Of Physics: Mass Defect

Introduction

If a particle combination contains extra energy, such as in a molecule of the explosive TNT, weighing it reveals some extra mass when compared to its end products after an explosion. (In theory, the extra mass must escape from the system as heat before its loss can be detected, so the end products must be weighed after they have been stopped and cooled.) If, on the other hand, energy is required to separate a system of particles into its constituents, the initial mass is less than the final mass of the constituents. In the latter case, the injected energy is “stored” as potential energy, which manifests as an increase in the mass of the components that store it. The energy that can be released by assembling lighter elements from lighter elements decreases and energy can be released when they fuse. This holds true for nuclei that are lighter than iron/nickel. More energy is required to bind heavier nuclei, and that energy can be released by breaking them up into fragments (known as atomic fission). At the moment, nuclear power is produced by breaking up uranium nuclei in nuclear power reactors and capturing the released energy as heat, which is then converted to electricity. In general, very light elements can fuse relatively easily, and very heavy elements can easily break up via fission; elements in the middle are more stable, and it is difficult to induce either fusion or fission in a laboratory environment.

The reason the trend reverses after iron is due to the increasing positive charge of the nuclei, which causes nuclei to break up. The strong nuclear interaction that holds nucleons together resists it. Although the electric force is weaker than the strong nuclear force, the strong force has a far smaller range: each proton repels the other 25 protons in an iron nucleus, but the nuclear force only binds close neighbours. As a result, electrostatic forces tend to dominate in larger nuclei, and the nucleus tends to split up over time.

Overview

The difference in mass between the actual atomic mass and the predicted mass calculated by adding the mass of protons and neutrons present in the nucleus is referred to as the mass defect. The actual atomic mass is less than the predicted mass calculated by adding nucleon masses. This extra mass is accounted for by binding energy, which is released during the formation of a nucleus. When a nucleus forms, some of its mass is converted to energy, resulting in the mass defect. As a result, the actual mass of an atomic nucleus is less than the mass of the particles that make it up. The actual mass of the atomic nucleus is always less than the mass of the nucleus’s protons and neutrons. Energy is released when a nucleus forms. This energy is removed as a reduction in total mass. This missing mass is referred to as the mass defect,’ and it is responsible for the energy released.

When an atom is broken down into its component particles, it is discovered that the atom’s mass is less than the sum of the masses of the component particles. The mass defect determines the difference between the masses. The mass defect also accounts for an atom’s stability. When an atom is broken down into its constituents, it is discovered that the total mass of the atom is less than the sum of its constituents’ masses. This means that the parent atom’s mass is less than the sum of its daughter atoms’ masses. When electrons and neutrons combine to form an atom, energy is released, which causes the atom to be stable. As a result, the sum of the masses of the constituent particles is less than the mass of the atom. The mass defect is defined as the difference between the sum of the masses of the constituent particles and the mass of the atom. The greater an atom’s mass defect, the more stable the atom.

The binding energy of an atom determines its stability, which is given by-

E=∆mc²

As a result, the mass defect is the difference between the sum of the masses of an atom’s component particles and the mass of the atom. The greater an atom’s mass defect, the more stable it is. Even in a motionless position, every object has a certain amount of energy, according to mass-energy equivalence. Kinetic energy does not exist in a stationary body. It simply holds prospective energy and probable chemical and thermal energy. The sum of all these energies, according to applied mechanics, is less than the product of the object’s mass and the square of the speed of light. When an item is at rest when it is not moving and has no momentum, the mass, and energy findings are similar and they can only be differentiated by one constant, namely the square of the light’s speed.

Binding energy of the nucleus

During the twentieth century, Albert Einstein, a well-known scientist, devised the breakthrough theory known as “the theory of relativity.” Mass and energy are interconvertible, according to the theory; mass can be turned into energy and vice versa. This additional dimension to physics aided in the resolution of many unsolved problems and provided a platform for many new hypotheses. One of them is the presence of Nuclear Binding Energy. As a result, nuclear mass and inter-nuclei interactions are now well understood.

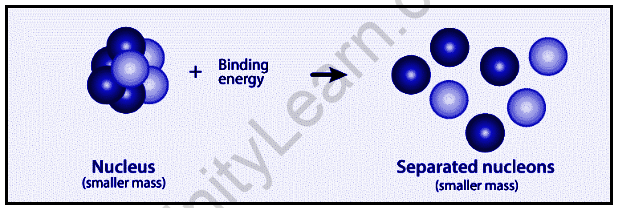
An atom is composed of a nucleus in the center and electrons that orbit around it in an orbital pattern. Nuclei are formed when protons and neutrons combine to form nuclei, which are referred to as nucleons. As a result, we expect the nucleus’ mass to be equal to the sum of the individual masses of neutrons and protons. However, this is not the case. The nucleus’ overall mass is smaller than the sum of the individual masses of neutrons and protons that make it up. This mass disparity is referred to as a mass defect.

∆m=Zm_p+(A-Z)m_n-m_nuc

The mass-energy relationship is equivalent, according to Einstein’s theory of relativity. In other words, the total energy of a system is determined by its mass. Given by the well-known equation E=mc². As a result, the total energy of the nucleus is implied to be less than the sum of the energies of individual protons and neutrons (nucleons). This means that as the nucleus disintegrates into constituent nucleons, some energy is released in the form of heat energy. (An exothermic reaction occurs.) The energy emitted here is expressed mathematically as.

E=(∆m)c²

Mass defect formula

The actual mass of the atomic nucleus is always less than the mass of the nucleus’s protons and neutrons. Energy is released when a nucleus forms. This energy is removed as a reduction in total mass. This missing mass is referred to as the mass defect,’ and it is responsible for the energy released.

The mass defect (M) is calculated by subtracting the original atomic mass (MA) from the total mass of protons,

(m_p=1.00728amu) and neutrons (m_n=1.00867 amu) the nucleus.

∆M=(Zm_p+Nm_n)-MA

Relation of mass and energy

According to mass-energy equivalence, all objects with mass, or massive objects, have corresponding intrinsic energy, even if they are stationary. In an object’s rest frame, where it is motionless and thus has no momentum, mass and energy are equivalent and differ only by a constant, the speed of light squared, In Newtonian physics, an immobile body has no kinetic energy, and it may or may not contain other types of stored energy, such as chemical or thermal energy, in addition to any potential energy it may have from its position in a field of force. These energies are typically much lower than the mass of the object multiplied by C², which is on the order of 10¹⁷ joules for a kilogram of mass.

Because of this principle, the mass of the atoms that exit a nuclear reaction is less than the mass of the atoms that enter, and the difference in mass manifests as heat and light with the same equivalent energy as the difference. Einstein’s formula can be used to analyze these explosions, with E representing the energy released and removed and m representing the change in mass.

According to the equation E=mc², an object’s energy is equal to its mass multiplied by the square of the speed of light. In other words, energy can be converted to mass and mass can be converted to energy.

The lower the energy level of an atom, the more stable it is. The mass defect follows the law of conservation of mass and energy. The binding energy of an atom is the amount of energy required to separate a particle from an atom system. The total binding energy is divided by the total number of nucleons to calculate the binding energy per nucleon.

Also read: Important Topic Of Physics: Radioactivity

FAQs

What causes widespread flaws?

Nuclear binding energy causes mass defects. This energy is solely responsible for the nucleons remaining together. This is accomplished through the exchange of virtual pions. The uncertainty principle is used to calculate their mass.

What is a nucleus's mass defect?

The mass defect of an atomic nucleus is the amount by which its mass differs from the sum of the masses of its constituent particles, and is the mass equivalent of the energy released during nucleosynthesis.