Introduction to Young’s Modulus

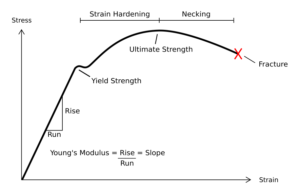
The stress-strain charts for various materials might seem very different. Brittle materials are robust because they can endure a great deal of stress, don’t extend much, and break quickly. The stress-strain relationship in ductile materials is linear in the elastic zone, but the linearity breaks down at the first turnover (the elastic limit), and the material could no longer return to its former form. The tensile strength is the second peak, and it informs us how much stress a material can bear before breaking. Plastic materials really aren’t particularly strong, yet they can withstand a great deal of stress. The gradient of the line in a stress-strain plot determines Young’s modulus.

Giordano Riccati, an Italian scientist, did the very first research using the notion of Young’s modulus through its modern incarnation in 1782, 25 years before Young’s study. The word modulus comes from the Latin word modus, which means measure.

What is Young’s Modulus?

Recognizing when an object or material will flex or break is one of the most critical tests in engineering, and the property that informs us of this is Young’s modulus. It is a measurement of a material’s ability to stretch and distort. The ratio of tensile stress to tensile strain is defined as Young’s modulus (E), a material parameter that tells us how easy it can stretch and flex. Where stress refers to the amount of force applied per unit area (F/A) and a strain refers to the amount of extension per unit length (d l/l). The Young’s modulus of a wire can be calculated by monitoring the change in length (d l) as weights of mass m are imposed (assuming g = 9.81 metres per second squared).

Young’s Modulus Formula:

E=σ/ϵ

E ≡ σ(ϵ)/ϵ =(F/A) / (ΔL/ L₀) = FL₀ /AΔL

The Young’s Modulus Formula has the following notations/units:

• E is Young’s modulus in Pa
• σ is the Uni axial stress of in Pa and
• ϵ is Strain or proportional deformation
• The object under strain exerts a force called F
• A is the cross-sectional area of the actual cross-section.
• ∆L denotes the length variation.
• The true length is L₀

Factors Affecting Young’s modulus:

1. We can assert that steel is more robust in nature than timber or polystyrene by studying its modulus of elasticity since it has a lower tendency to deform under applied load. Young’s modulus is also used to calculate how often a material will deform when subjected to a given load.
2. Another thing to remember is that the lower Young’s Modulus of a material, the greater the deformation suffered by the body, and in the case of clay and wood, this distortion might vary within a single sample. One side of the clay sample deforms more than the other, whereas a steel bar deforms evenly all the way around.

Young’s Modulus Characteristics:

• One of the most important tests in engineering is determining when an object or material will bend or break, and the characteristic that tells us this is Young’s modulus.
• The ratio of tensile stress () to tensile strain () is defined as Young’s modulus (E), a material property that indicates how easily it can stretch and flex.
• The stress-strain curves for several materials may appear to be quite dissimilar. Brittle materials are exceptionally strong since they can withstand a great deal of stress, stretch little, and fracture quickly. Plastic materials are not particularly durable, but they can withstand a lot of stress. Young’s modulus is represented by the gradient of a line in a stress-strain diagram.
• Material mechanical characteristics research is important in helping us understand how the material will react and helps to create new products and improve existing ones.
• On a microscale, many things comprise both biological and non-biological microparticles (e.g., pharmacological drugs, reproductive therapies, tissue engineering) (e.g., chemicals, agriculture, household care). We can foresee their behavior in manufacturing and processing by understanding their mechanical properties, allowing us to maximize their performance potential.
• A material’s Young’s modulus is a crucial property to know in order to predict how it will react when subjected to a force. This is crucial for virtually everything in our environment, including buildings, bridges, autos, and more.
• A substance’s Young’s Modulus is an immutable fundamental property of all materials. Temperature and pressure, on the other hand, play a role.
• The stiffness of a material is defined by its Young’s Modulus (or Elastic Modulus). To put it another way, how easily it bends or stretches.

Concepts on Young’s Modulus:

1. A material’s Young’s modulus is a valuable feature to grasp in order to forecast how it will behave when applied to a force. This is significant for practically all in our environment, namely buildings, bridges, vehicles, and more.
2. The stress-strain curve is linear at near-zero stress and strain, and Hooke’s law, which asserts that stress is proportional to strain, describes the connection between stress and strain. Young’s modulus is the proportionality coefficient.
3. The higher the modulus, the more the stress is required to produce the same amount of strain; in an idealized rigid body, Young’s modulus would be infinite. A really soft substance (such as a fluid) on the other hand, could deform zero force and have zero Young’s modulus.

Significance of Young’s modulus in NEET exam:

In engineering and materials science, a stress-strain curve for material is being used to depict the stress-strain-strain- strain relationship. It’s calculated by gradually increasing the load on a test coupon and measuring deformation, which can then be used to calculate stress and strain. Stress-strain curves depict the displacement of a substance in response to a tensile, compressive, or torsional force. When evaluating various materials based on how they react to various loads, this is extremely important. Mechanical properties are the physical attributes that a substance exhibits when it is subjected to forces. Mechanical properties comprise modulus of elasticity, tensile strength, elongation, toughness, and fatigue limit. The mechanical properties of the material would be those that control how it responds to applied loads.

Students should study all of the major chapters of the NEET curriculum to get the best results on the NEET test. Infinity Learn’s important questions for NEET are one of the most trustworthy study aids because they cover all of the main concepts in the syllabus. Additionally, these crucial questions are created from previous year’s question papers, taking into account the importance of each chapter in the curriculum.

Physics is one of the most significant courses for the NEET entry exam, and it is a required topic for which you must study. Infinity learn makes it easier to study Physics for NEET; the revision notes provided by infinity learn experienced staff is the best notes available for the Physics subject young’s modulus. Young’s modulus NEET Big Problems can be downloaded for free to help you prepare for your final exam.

FAQs on Youngs Modulus

Name an example of the material which has the most elasticity.

Steel is one of the materials with the greatest flexibility.

What exactly is ductility?

Ductility is indeed the material property that allows it to be pulled to a smaller portion when tensile stress is applied

Young's modulus SI unit is measured by?

The SI unit for Young's modulus is Pascal.

What really do you imply whenever you mention elastic modulus?

The stress-to-strain ratio below the limit of proportionality is defined as elastic modulus. It is a measurement of the rigidity or stiffness of a substance. The stiffer the material is, or the lower the elastic strain induced by a given load, the higher the modulus.