Table of Contents
Linear momentum is the vector amount and is characterized as the result of the mass of an item, m, and its speed, v. The letter ‘p’, is applied to communicate it and utilized as a force for short. It is to be noticed that the body’s energy is generally in similar bearing as its speed vector. It’s a saved amount which implies that the complete force of a framework is steady. Linear momentum is measured in kilograms per second.
The Linear momentum recipe is given by,
P = m v
Where,
m = mass
v = velocity
How momentum and net force are related?
You might recall from the kinematic equations with constant acceleration that change in velocity △v can also be written as a△t. Therefore, any change in momentum following an acceleration can be written as
△p= m△v
=m(a△t)
=F net△t
If we rearrange this to solve for F net when the mass of the system and the net force is constant, we get Newton’s second law
F net= △p/△t
Consequently, the adjustment of energy after some time is equivalent to the net power. A greater net power throughout a similar time span implies a bigger change in energy. For instance, a weighty truck grinding to a halt will have a lot bigger change in energy than a light vehicle in a similar measure of time. A bigger change in energy implies a bigger outside power is expected to dial it back, so the truck brakes need to work a lot harder!
Law of conservation of Linear Momentum
The law of conservation of energy is perhaps the most conspicuous law in physics. The conservation of energy law standards lets us know that the all-out force of a framework is saved all the time. Allow us to look into the protection of force with the assistance of determination and a few settled models.
Law of conservation of energy expresses that:
For at least two bodies in a disengaged framework following up on one another, their all-out energy stays consistent except if outside power is applied. Thus, energy cannot be made nor annihilated.
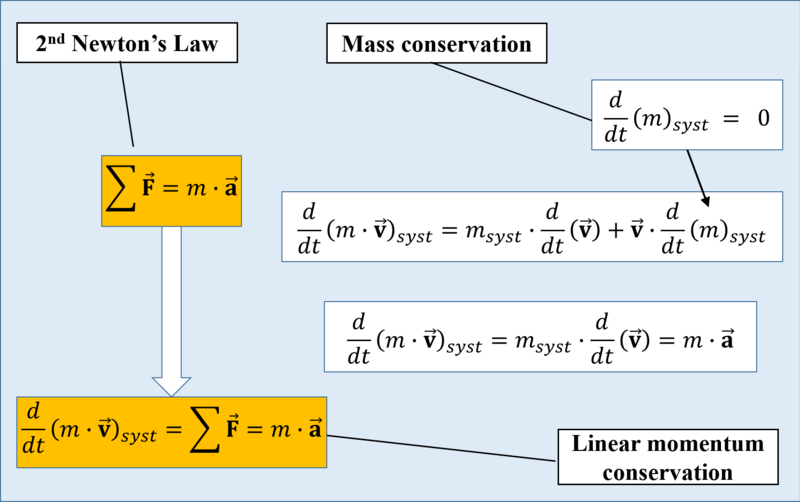
Derivation of Law of Conservation of Linear Momentum
Newton’s third law states that when object A applies force to object B, object B applies back an equal force in magnitude, but in the opposite direction. Newton used this concept to derive the law of conservation of momentum.
Let A and B be two colliding particles with masses of m 1 and m 2 and initial and final velocities of u 1 and v 1 and u 2 and v 2 respectively. t is the time between two particles when they come into contact.
Change in momentum of particle A = m 1(v 1 – u 1)
B = m 2( v 2 – u 2) (transformation of the momentum of the particle B)
FBA = -FAB (According to the third law of motion)
FBA = m 2 × a 2 = m 2 (v 2 – u 2) / t
FAB = m 1 × a 1 = m 1(v 1 – u 1)/t x m 2(v 2 – u 2)/t
= -m 1 (v 1 – u 1)/t
m 1 u 1 + m 2 u 2 = m 1 v 1 + m 2 v 2
As a result, above is the equation for the law of conservation of momentum where m1u1 + m2u2 is the representation of the total momentum of particles A and B before and after a collision where m1v1 + m2v2 represents the total momentum of particles A and B after a collision.
Examples of Law of Conservation of Linear Momentum
Following are the examples of the law of conservation of momentum:
- Air-filled balloons
- System of gun and bullet
- Motion of rockets
A solution to a problem on Law of Conservation of Momentum
Q 1. Cars that weigh 4 kilograms and 10 kilograms respectively are at rest. Suppose a car has a mass of 10 kg and moves towards the east at a speed of 5 m.s.-1. Find the velocity of the car with a mass of 4 kg with respect to the ground.
Ans: Given,
m 1 = 4 kg
m 2 = 10 kg
v 1 = ?
v 2 = 5 m.s-1
Based on the conservation of momentum, we know that:
P initial = 0, since the cars are stationary
P final = p 1 + p 2
P final = m 1. v 1 + m 2. v 2
= 4 kg. v 1 + 10 kg.5 m.s-1
Pi = Pf
0=4 kg. v 1+50 kg.m.s-1
v 1 = 12.5 m.s-1
Constant linear momentum and its applications
- Rocket Launch: At the point when the rocket is sent off, the consuming fuel launches from the lower end of the rocket, which powers the rocket machine to move the other way of the fuel catapulted. The mass of the rocket continues diminishing alongside the consumption of the fuel because of which the energy of the rocket continues to increment. The all-out force of the framework, including rocket and fuel, continues as before the repugnance of the rocket.
- An explosion of a bomb: Assume a bomb is very still before it detonates. Its force is zero. At the point when it detonates, it separates into many parts, each part having a specific force. A section flying in one heading with a specific force, there is another part moving the other way with similar energy. Assuming that the bomb detonates into halves, they will take off in precisely inverse bearings with a similar speed, since each part has a similar mass.
Conservation law, additionally called the law of conservation, in material science, is a rule that expresses that specific actual property (i.e., a quantifiable amount) doesn’t shift in the direction of time inside a segregated actual framework. In traditional material science, laws of this kind govern energy, force, angular force, mass, and electric charge. In molecule material science, other protection laws apply to properties of subatomic particles that are invariant during communications. A significant capacity of protection laws is that they make it conceivable to foresee the plainly visible conduct of a framework without thinking about the minuscule subtleties of the course of an actual cycle or substance response.
Also read: Fundamental and Derived Units
Frequently Asked Questions
Question: The law of conservation of momentum can be illustrated with some examples.
Answer: Examples of the law of conservation of momentum are:
- Motion of rockets
- Air-filled balloons
- System of gun and bullet
Question: Momentum is a scalar or a vector quantity?
Answer: The magnitude and direction of the quantity make it a vector quantity.
Question: Does friction affect the conservation of momentum?
Answer: Yes, friction affects momentum. As friction increases, momentum decreases.
Cracking NEET 2023 will no longer be a challenge. Our Result-Oriented Learning Program at Infinity Learn will place you in the category of the top rankers.
Kickstart your NEET Exam Preparation with Infinity Learn. Get taught by our top teachers for the NEET Entrance Exam and join the league of NEET toppers.
