Table of Contents
Introduction:
Motion in a vertical circle is a type of motion that involves an object moving in a circular path along a vertical plane, typically under the influence of gravity. Because of the gravitational attraction, a vertical circular motion is called non-uniform because the velocity and tension of objects will differ in amplitude in different directions.
When an object in a vertical circle is released from a height, its motion descends vertically to the earth’s surface. The earth’s gravitational force is responsible for this. The related acceleration is called acceleration owing to gravity and is denoted by the letter g. This means that all bodies, regardless of their physical attributes, should fall to the ground at the same time. At the bottom of the circle, all objects have the same velocity, and the rope or thread gets slack at the top.
ac = ∑ f c/m
ac = circular acceleration
∑ f c = the total force applied
m = the mass of the object
A brief outline:
Gravity must be included while examining the motion of a body in a vertical circle. Due to the influence of the earth’s gravitational field, the magnitudes of the body’s velocity and tension in the string alter continuously. It is greatest in the lowest position and minimal in the highest position. As a result, a vertical circle’s circular motion is not uniform.
The velocity of a Body Moving in a Vertical Circle is an expression of the speed with which a body moves in a vertical circle. Consider a small body with mass m whirled in a vertical circle with radius t by one end of a string. In this example, the body’s acceleration increases as it descends the vertical circle and drops as it ascends it.
As a result, the body’s pace fluctuates constantly. At the base of the vertical circle, it achieves its maximum, and at the top, it reaches its minimum. As an outcome, the body no longer moves in a circular motion. Irrespective of where the particle is on the circle, the weight ‘mg’ always functions vertically downward.
Important concepts:
A Particle’s Motion in a Vertical Circle: When a body is released from a great height, it descends vertically to the earth’s surface.
This occurs as a result of the earth’s gravitational influence on the body. The acceleration caused by this force is known as gravity acceleration and is symbolized by the letter ‘g.’ The value of ‘g’ on the earth’s surface is set to 9.8 m/s 2, which is the same for all bodies.
It signifies that all bodies (whether an iron ball or a piece of paper) should fall at the same speed and take the same amount of time to reach the earth when dropped from the same height (u = 0). It is the minimal velocity supplied to the particle at the lowest point to complete the circle. When the particle is at the highest point of the circle, the string’s inclination to become slack is greatest.
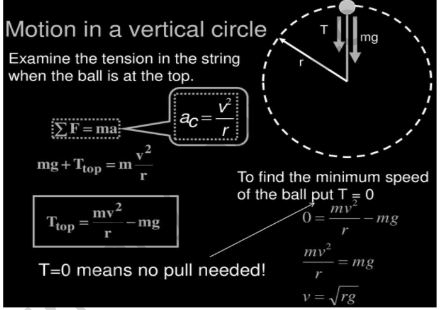
On the topmost, tension is specified by T = m v T 2/R – mg,
where v T = speed of the particle at the topmost.
m v T 2/R = T + mg
For v T to be smallest, T=0
VT = √g R
If VB be the critical velocity of the particle at the bottom-most,
then from conservation of energy theory:
Mg(2 R) + 1/2 m v T 2 = 0 + ½ m v B 2
As v T = √g R > 2 m g R + ½ m g R
= ½ m v B 2
So v B=5 g R
Highest point H(h=2 r)
We have, v = √u 2−2 g h
v = √(5 gr)2−2 g(2 r)
v = √5 gr−4 gr
= √gr
Tension at the lowermost point:
T− mg = m v 2/R……..(since v = √5 gr)
T = 6 mg
Tension at highest point:
T + mg = m v 2/R …….(since, v = √gr)
T=0
An object travelling in a vertical circle is a common example of circular motion. Roller coasters, cars on winding roads, and a bucket of water on a string are all examples. As the bucket and roller coaster go, they turn totally upside down, which differs from the scenario of the vehicle on the street, which (hopefully) remains upright.
Significance of motion in a vertical circle for NEET exam:
The study of motion in a vertical circle is the subject of physics. The NEET test covers all of these areas. They’re covered in depth in the NCERT Physics textbook, which was developed exclusively for the NEET exam. Students can learn about such notions as well as the derivation of several formulas related to them by visiting the Infinity Learn website. In the chapter’s exercises, there are also various issue problems to help you practice and understand the topic’s application. Students can also study other publishers’ physics textbooks.
Frequently asked questions (FAQs):
Question 1: What is the definition of a vertical circular motion? Demonstrate that the motion of an object rotating in a vertical circle isn’t uniform.
Answer 1: When a body circle body circles in a vertical circle and its motion at different points differs, the motion is described as vertical circular motion. Consider a mass m object whirling in a vertical radius of radius r by a mass m object whirled in a vertical radius of radius r by a mass m object whirled in a vertical radius of radius r by a mass m object whirled in a vertical radius of radius r by a mass m object. The body’s velocity and tension fluctuate in magnitude from a maximum at the base point to minimal at the top (highest) point due to the impact of the earth’s gravitational field. As a result, non-uniform circular motion occurs as the body moves in a vertical circle.
Question 2: Is it possible to have a uniform circular motion in a vertical circle?
Answer 2: No, the velocity will change due to gravity amid circular motion, so will not be uniform.” i
Question 3: Define circular motion and circular motion that is uniform.
Answer 3: Circular motion is regarded as the moving object along a circular route. Uniform circular motion is defined as an item travelling along a circular path that covers the same distance in the same amount of time.
Key cases
Case 1: Whenever the body is at lower site (h = 0)
T = m ⁄ r (u 2 – 3 g h + g r)
At this point L (h = 0)
TL = m ⁄ r (u 2 – 3 g (0) + g r)
= m ⁄ r (u 2 + g r)
Case 2: Whenever the body is at upper position (h = 2 r)
T = m ⁄ r (u 2 – 3 g h + g r)
At this point H (h = 2 r)
TH = m ⁄ r (u 2 – 3 g (2 r) + g r)
= m ⁄ r (u 2 – 5 g r)
Case 3: Whenever the string is horizontal (h = r)
T = m ⁄ r (u 2 – 3 g h + g r)
At this point M (h = r)
TM = m ⁄ r (u 2 – 3 g (r) + g r)
= m ⁄ r (u 2 – 2 g r)
Association among tension at the high point and at the low point
TL – TH = m ⁄ r (u 2 + g r) – m ⁄ r (u 2 – 5 g r)
= m u 2 ⁄ r + mg – m u 2 ⁄ r + 5 mg
= 6 mg
As a consequence, the string’s tension at the lowest level L is six times greater than the string’s tension at the top position H.
Infinity Learn App
Now you can find answers to all your subject queries & prepare for your Exams on our Learning App – Infinity Learn.







