Table of Contents
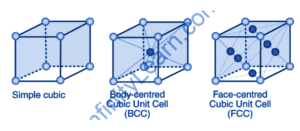
Cubic Unit Cell: A crystal structure is an ordered arrangement of atoms, ions, and molecules described in a Crystalline material. Ordered structures occur when the nature of particles shape up in a symmetrical pattern that repeats with the primary direction of matter in three-dimensional space. The structure and symmetry of the entire crystal are mirrored by the unit cell’s repetitive translation with its principal axis. Lattice constants are the lengths of the principal axes and the angles of the unit cell. They’re referred to as cell parameters or lattice parameters. The concept of the space group defines the symmetry properties of the crystal.
Crystal structure and symmetry are important in defining a variety of physical properties such as cleavage, optical transparency, and electronic band structure. A unit cell is defined as the smallest repeating unit of the crystal lattice in a living organism, as well as the crystal’s building block. That is how life began to exist on Earth. Within a crystal structure, atoms are arranged in three-dimensional symmetry. A crystal structure is defined as the geometric arrangement of particles in a unit cell. The geometry of the unit cell is known as a parallelepiped. It provides six lattice parameters that represent the length and angles of the cell edges.
Overview
Fractional coordinates are used to represent the particle’s position in the unit cell. They are measured with the cell’s edges as a reference point. It is critical to report the coordinates of particles from the smallest asymmetric subset. These particles are chosen to occupy the smallest physical space, demonstrating that it is not necessary for all particles to be physically located within the boundaries provided by lattice parameters. The other particles of a unit cell are created by the symmetry operations that describe the symmetry of the unit cell. The Crystal structure’s space group is defined as the collection of unit cell symmetry operations. The Crystal structure’s atom group is the same, the basis, and they are stationed around each and every lattice point. In nature, there are three types of unit cells: primitive cubic, body-centred cubic, and face-centred cubic. The Crystal structure’s atom group is the same, the basis, and they are stationed around each and every lattice point. In nature, there are three types of unit cells: primitive cubic, body-centred cubic, and face-centred cubic.
The identical unit cells are defined in such a way that they fill space without overlapping. A crystal lattice is the three-dimensional arrangement of atoms, molecules, or ions within a crystal. It is made up of a large number of unit cells. Every lattice point is occupied by one of the three constituent particles. A primitive cubic, body-centred cubic (BCC), or face-centred cubic unit cell can exist (FCC). In this section, we will go over the three different types of unit cells in depth.
A crystal lattice is formed by the interconnection of many unit cells. Atoms and molecules are also constituent particles. One of these particles occupies each lattice point.
- Cubic Unit Cell, Primitive
- Cubic Unit Cell with a Body
- Cubic unit cell with a face on it
The cubic unit cell (primitive)
Atoms are only present at the corners of a primitive cubic unit cell. Every atom in the corner is shared by eight neighbouring unit cells. Four unit cells are in the same layer, and four are in the upper (or lower) layer. As a result, each unit cell contains only 1/8th of an atom.
Cubic unit cell centred on the body
A body-centred cubic unit cell has atoms at each corner and an atom in the centre.
Cubic unit cell with a face on it
A face-centred cubic unit cell has atoms at all of the crystal lattice’s corners and in the centre of all of the cube’s faces. The atom in the face-center is shared by two adjacent unit cells, and only 12 of each atom is assigned to a unit cell.
The effective number of atoms per unit cell
In a simple cubic, face-centred cubic, and body-centred cubic, the number of atoms per unit cell is 1,4,2.
(1) One simple cubic unit cell of a monoatomic substance contains one atom.
A simple cubic unit cell has 8 atoms at each of its eight corners. Each atom adds one eighth to the unit cell. The contribution total is 1.
(2) For the FCC 8 corners 1/8 per atom
= 8× 1/8
= 1 atom
b) 6 face-centred atoms 1/2 atom per unit cell = 3 atoms,
As a result, the total number of atoms in a unit cell equals four. As a result, we have the following in a face-centred cubic unit cell:
8 corners, 1/8 per corner atom
= 8 corners, 1/8 per corner atom
= 8 corners, 1/8 per corner atom
= 8 corners, 1/8 per corner atom
= 8 corners, 1/8 per corner
6 face-centred atoms divided by 1/2 atom per unit cell equals 3 atoms As a result, the total number of atoms in a unit cell is four.
(3) One body-centred cubic unit cell of a monoatomic substance contains two atoms. A bcc unit cell has 8 atoms at each of its eight corners.
Each atom adds one eighth to the unit cell. The contribution total is 1.
A bcc unit cell has one atom in its body centre. The atom makes a complete contribution to the unit cell.
The total contribution is 1. The total number of atoms in a single fcc unit cell is 1+1=2.
FAQ’s
What is a unit cell and what are the different types?
A unit cell is the smallest replicating portion of a crystal lattice. There are numerous types of unit cells. For example, the cubic crystal structure has three distinct unit cell types: (1) plain cubic, (2) face-centred cubic, and (3) body-centred cubic.
What exactly do you mean when you say primitive unit cell?
In mathematics, biology, mineralogy (especially crystallography), and solid-state physics, a primitive cell (also known as a primitive unit cell) is a minimum-volume unit cell referring to a single lattice point of a structure with discrete translation symmetry. The main cell is straightforward.
What exactly is a Primitive Unit Cell?
A primitive cell is a cell unit that contains exactly one lattice point. It is the smallest possible cell in terms of size. However, if a lattice point is present at the cell's very edge and it is shared with another cell, it will only count on behalf of that cell. Furthermore, if a point is located on the cube's corner, it is shared by 8 cubes, and the count is 18. With crystal translation operations, a cell will always try to fill the lattice space without leaving any gaps.







