Table of Contents

Introduction
A Unit Cell can be thought of as a three-dimensional structure made up of one or more atoms. Regardless of the cell’s packing, some void space is always present. The packing fraction is the fraction of total space that is filled with the inherent constituent particles of a specific cell or structure. It is calculated by dividing the total volume occupied by constituent particles by the total volume of the cell. When expressed as a percentage, the percentage of total space held up by constituent particles is referred to as the Packing Efficiency of a Unit Cell.
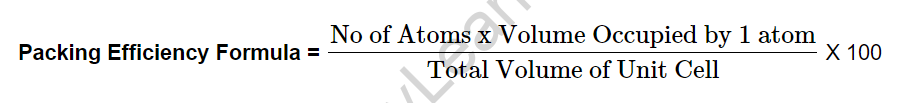
In terms of packing, both ccp and hcp are highly efficient lattices. Both types of close-packed structures have a packing efficiency of 74%, which means that 74% of the space in hcp and ccp is filled. In terms of packing, the hcp and ccp structures are both equally efficient.
Packing efficiency is defined as the percentage of a solid’s total volume occupied by spherical atoms. The formula is written as “s3 is the ratio of one atom’s volume to the volume of cells.” The packing efficiency equation can be written mathematically as Volume obtained by 1 share of the number of atoms / Total volume of unit cell 100 per cent. The percentage ratio of space obtained by constituent particles packed within the lattice is defined as packing efficiency.
Overview
A crystal lattice is made up of a large number of unit cells, with one constituent particle occupying each lattice point. The unit cell is a three-dimensional structure that contains one or more atoms. Regardless of the type of packing, we always find some void spaces in the unit cell. The packing fraction of a unit cell is the percentage of spaces filled by the particles in the unit cell.
This section will teach us about packing efficiency. Packing Efficiency is defined as the percentage of total space in a unit cell that is filled by constituent particles packed within the lattice, such as atoms, ions, or molecules. It is the total amount of space that these particles occupy in three-dimensional space. Simply put, it is the specified percentage of a solid’s total volume that is occupied by spherical atoms. With the help of geometry, packing efficiency can be assessed in three structures:
- Cubic Close Packing and Hexagonal Close Packing are two types of close packing.
- Body-Centred Cubic Structures
- Cubic Simple Lattice Structures
The following factors influence a unit cell’s packing efficiency. A lattice structure’s number of atoms.
- A unit cell’s volume.
- Atomic volume
- The Value of Packing Efficiency
- Packing efficiency is critical because:
- Packing Efficiency represents the object’s solid structure.
- It exhibits solid properties such as consistency, density, and isotropy.
- Packing Efficiency can be used to derive various attributes of solid structures.
Atomic packing factor for simple cubic
The fraction of volume in a crystal structure occupied by constituent particles is referred to as the atomic packing factor (APF), packing efficiency, or packing fraction in crystallography. It is a dimensionless number that is always less than one. In atomic systems, the APF is calculated by assuming that atoms are rigid spheres. The radius of the spheres is set to the maximum value that will prevent the atoms from overlapping. The packing fraction of one-component crystals (those containing only one type of particle) is represented mathematically by

The number of atoms per unit cell in a simple cubic packing is one. The length of the unit cell’s side is 2r, where r is the radius of the atom.
Calculate packing efficiency of the simple cubic unit cell
Atoms are located at the cube’s corners in a simple cubic unit cell. Consider a unit cell with edge length “a.” Atomic radius can be expressed as,
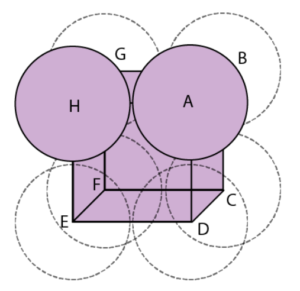
r =
=> a = 2r
Each unit cell in a simple cubic structure contains only one atom.

FAQ’s:
Question 1: What exactly is packing efficiency?
Answer 1: Packing efficiency is the percentage of total space occupied by particles in a particular packing. In the crystal lattice, the constituent particles, such as atoms, ions, or molecules, are densely packed. They can do so using either cubic close packing (ccp) or hexagonal close packing (hcp) (hcp). In both cases, a number of free spaces or voids are left, indicating that the entire space is not occupied.
Question 2: How efficient is the packing in the HCP and CCP structures?
Answer 2: Hexagonal close packing (hcp) and cubic close packing (ccp) both have a packing efficiency of 74%.
Question 3: How efficient is SCC’s packing?
Answer 3: Simple cubic unit cell (SCC) packing efficiency is 52.4 per cent.







