Table of Contents
Trigonometry is a branch of mathematics that uses specific formulas to solve various types of problems. These problems often involve trigonometric ratios like sine, cosine, tangent, secant, cosecant, and cotangent, as well as Pythagorean and product identities.
Additionally, there are formulas that deal with the signs of ratios in different quadrants, cofunction identities (which involve shifting angles), sum and difference identities, double angle identities, and half-angle identities.
For students in Classes 10, 11, and 12, learning and memorizing these trigonometry formulas is crucial for achieving good grades in this subject. These formulas can be found in a trigonometry table, along with inverse trigonometry formulas, which are helpful for solving related problems.
Trigonometry Formulas PDF
Trigonometry, a branch of math focused on triangles, explores the connections between triangle sides and angles. Its formulas find extensive practical applications.
For instance, it’s vital in Geography for measuring distances between landmarks, in Astronomy for determining star distances, and in satellite navigation systems. Download free PDF Trigonometry formulas to study offline and enhance your math skills.
Trigonometry Formulas List
When we talk about trigonometric formulas, we mainly focus on their application to right-angled triangles. In a right-angled triangle, there are three important sides: the longest one is called the hypotenuse, the side opposite to the angle is known as the perpendicular, and the side where both the hypotenuse and perpendicular side meet is called the adjacent side.
Now, let’s take a look at some important trigonometry formulas:
Basic Formulas
In trigonometry, there are six essential ratios known as trigonometric functions. These functions help us understand the relationships between the sides of a right-angled triangle. Here are the six trigonometric functions and their corresponding formulas:
- Sine (sin θ) = Opposite Side / Hypotenuse
- Cosine (cos θ) = Adjacent Side / Hypotenuse
- Tangent (tan θ) = Opposite Side / Adjacent Side
- Secant (sec θ) = Hypotenuse / Adjacent Side
- Cosecant (csc θ) = Hypotenuse / Opposite Side
- Cotangent (cot θ) = Adjacent Side / Opposite Side
These functions are fundamental in trigonometry and are used to solve various problems involving angles and triangles.
Reciprocal Identities
Here are the reciprocal trigonometric identities and their explanation:
- Cosecant (csc) is the reciprocal of sine (sin):
csc θ = 1/sin θ
- Secant (sec) is the reciprocal of cosine (cos):
sec θ = 1/cos θ
- Cotangent (cot) is the reciprocal of tangent (tan):
cot θ = 1/tan θ
- Sine (sin) is the reciprocal of cosecant (csc):
sin θ = 1/csc θ
- Cosine (cos) is the reciprocal of secant (sec):
cos θ = 1/sec θ
- Tangent (tan) is the reciprocal of cotangent (cot):
tan θ = 1/cot θ
These identities are used in trigonometry, typically in the context of right-angled triangles. When you know the lengths of the triangle’s sides, you can use these formulas to find the values of sine, cosine, tangent, secant, cosecant, and cotangent for a given angle θ. These reciprocal trigonometric identities are derived based on the relationships between trigonometric functions.
Trigonometry Table
Here’s a handy table of commonly used trigonometry formulas for solving angle-related problems.
| Trigonometry Table | ||||||||
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (In Radians) | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Periodicity Identities
These formulas help us change the angles in trigonometry by specific amounts like π/2, π, 2π, and more. They are also known as co-function identities.
- sin (π/2 – A) = cos A & cos (π/2 – A) = sin A
- sin (π/2 + A) = cos A & cos (π/2 + A) = – sin A
- sin (3π/2 – A) = – cos A & cos (3π/2 – A) = – sin A
- sin (3π/2 + A) = – cos A & cos (3π/2 + A) = sin A
- sin (π – A) = sin A & cos (π – A) = – cos A
- sin (π + A) = – sin A & cos (π + A) = – cos A
- sin (2π – A) = – sin A & cos (2π – A) = cos A
- sin (2π + A) = sin A & cos (2π + A) = cos A
All these trigonometric identities follow a repeating pattern, called periodicity. However, each identity has its own unique periodicity constant. For example, tan 45° is the same as tan 225°, but this is also true for cos 45° and cos 225°. You can refer to the table above for the values and verify them.
Cofunction Identities
Co-function or periodic identities can also be expressed in degrees as follows:
- sin(90°−x) = cos x
- cos(90°−x) = sin x
- tan(90°−x) = cot x
- cot(90°−x) = tan x
- sec(90°−x) = cosec x
- cosec(90°−x) = sec x
Sum & Difference Identities
The sum and difference identities in trigonometry are formulas that express the sine, cosine, and tangent of the sum or difference of two angles in terms of the sine, cosine, and tangent of the individual angles. These identities are useful in simplifying trigonometric expressions and solving trigonometric equations. Here are the sum and difference identities for sine, cosine, and tangent:
- sin(A + B) = sinA cosB + cosA sinB
- sin(A – B) = sinA cosB – cosA sinB
- cos(A + B) = cosA cosB – sinA sinB
- cos(A – B) = cosA cosB + sinA sinB
- tan(A + B) = (tanA + tanB) / (1 – tanA tanB)
- tan(A – B) = (tanA – tanB) / (1 + tanA tanB)
These identities can be extremely helpful when you need to simplify trigonometric expressions, solve trigonometric equations, or manipulate trigonometric functions involving the sum or difference of angles. They are derived from the basic trigonometric definitions and the Pythagorean identities.
Double Angle Identities
Double angle identities in trigonometry are mathematical relationships that express the trigonometric functions of twice an angle in terms of the trigonometric functions of the angle itself.
These identities can be useful in simplifying trigonometric expressions and solving trigonometric equations. Here are the double-angle identities for the sine, cosine, and tangent functions:
- sin 2A = 2 sin A cos A (or) (2 tan A) / (1 + tan2A)
- cos 2A = cos2A – sin2A (or) 2cos2A – 1 (or) 1 – 2sin2A (or) (1 – tan2A) / (1 + tan2A)
- tan 2A = (2 tan A) / (1 – tan2A)
Triple Angle Identities
Triple angle identities in trigonometry are formulas that express trigonometric functions of three times an angle (θ) in terms of trigonometric functions of the angle itself. These identities are useful for simplifying trigonometric expressions and solving trigonometric equations. Here are the triple angle identities for the sine, cosine, and tangent functions:
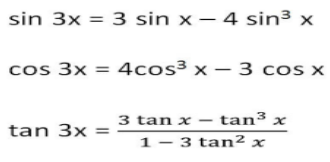
Half Angle Identities
The half-angle identities in trigonometry are a set of formulas that express trigonometric functions of half an angle in terms of trigonometric functions of the original angle. These identities are useful in various trigonometric calculations and simplifications.
There are several half-angle identities, and they are derived from the double angle identities. Here are the most commonly used half-angle identities:
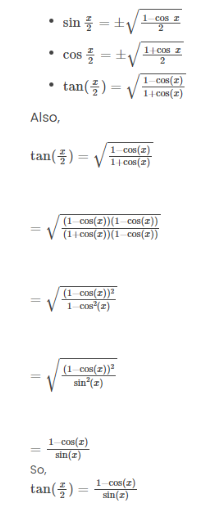
Sum to Product Identities
The sum-to-product identities in trigonometry are formulas that express the sum or difference of two trigonometric functions in terms of their products. These identities are useful for simplifying trigonometric expressions and solving trigonometric equations. There are the following sum-to-product identities:
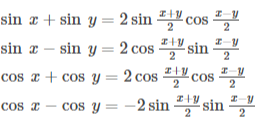
Inverse Trigonometry Formulas
- sin-1 (–x) = – sin-1 x
- cos-1 (–x) = π – cos-1 x
- tan-1 (–x) = – tan-1 x
- cosec-1 (–x) = – cosec-1 x
- sec-1 (–x) = π – sec-1 x
- cot-1 (–x) = π – cot-1 x
Trigonometry Formulas FAQs
What is Trigonometry?
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It involves the study of trigonometric functions like sine, cosine, tangent, and their applications
Why are Trigonometry Formulas Important?
Trigonometry formulas are important because they help us solve various types of problems involving angles and triangles. They have practical applications in fields such as physics, engineering, astronomy, and navigation.
What Are the Basic Trigonometric Functions?
The basic trigonometric functions are sine (sin), cosine (cos), tangent (tan), secant (sec), cosecant (csc), and cotangent (cot). They relate the angles and sides of right-angled triangles.
What Are Reciprocal Trigonometric Identities?
Reciprocal trigonometric identities relate the reciprocals of the basic trigonometric functions. For example, cosecant (csc) is the reciprocal of sine (sin), and secant (sec) is the reciprocal of cosine (cos)
How Can I Remember Trigonometry Formulas?
Mnemonics and memory aids can be helpful in remembering trigonometry formulas. Additionally, practice and application of these formulas in solving problems can reinforce your memory.









