Table of Contents
Trigonometry formulas are essential mathematical tools that deal with the connections between triangle angles and sides. These formulas, which include sine, cosine, tangent, and their inverses, allow us to handle a variety of real-world distance, height, and angle issues. Understanding and navigating the world around us is made easier by mastering trigonometric formulae.
List of Important Trigonometry Formulas
Let’s explore trigonometry formulas. Imagine you have a right-angled triangle. This triangle has an angle, which we’ll call θ, a longest side called the hypotenuse, a side that’s right next to θ called the adjacent side, and another side that’s across from θ, which we’ll call the opposite side.
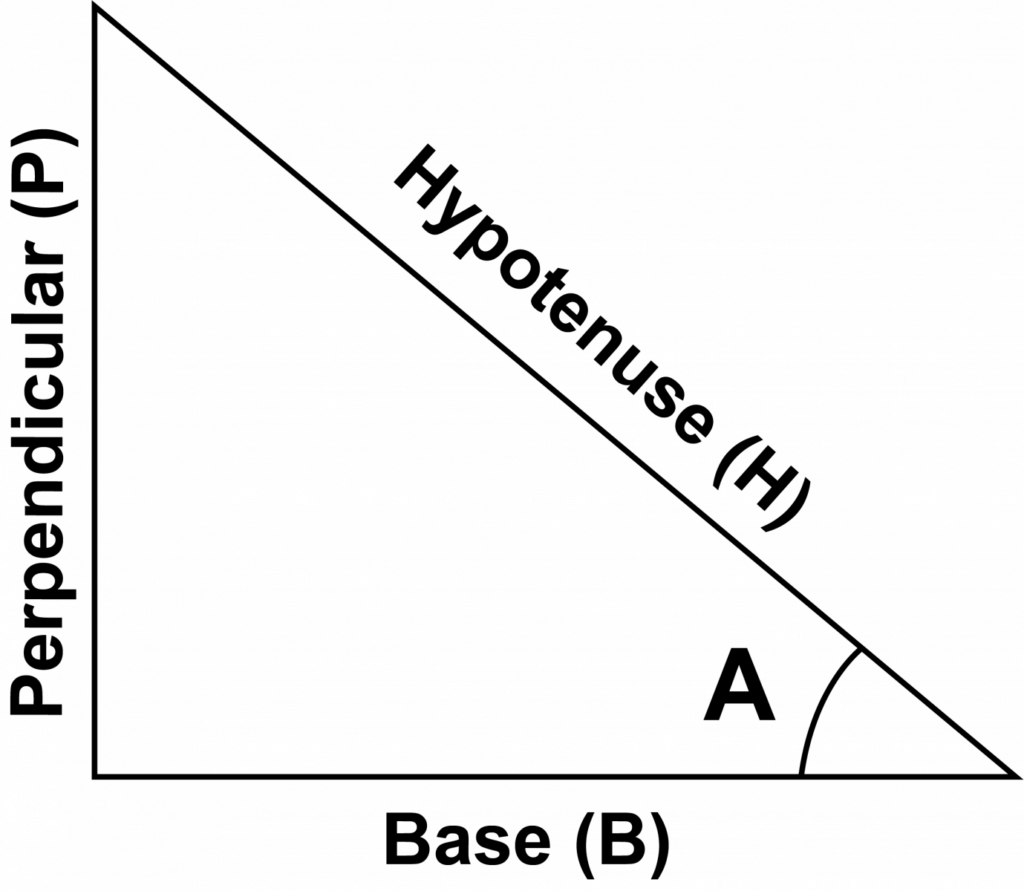
Basic Trigonometric Ratios
- sinθ = Opposite side / Hypotenuse
- cosθ = Adjacent side / Hypotenuse
- tanθ = Opposite side / Adjacent Side
- secθ = Hypotenuse / Adjacent side
- cosecθ = Hypotenuse / Opposite side
- cotθ = Adjacent Side / Opposite side
Trigonometric Identities
Trigonometric identities are special equations that connect various trigonometric functions like sine, cosine, and tangent. They help simplify expressions and solve trigonometric problems.
Reciprocal identities
- sinθ = 1/cosecθ
- cosecθ = 1/sinθ
- cosθ = 1/secθ
- secθ = 1/cosθ
- tanθ = 1/cotθ
- cotθ = 1/tanθ
Trigonometry Identities
Tangent and Cotangent Identities
- tanθ = sin θ / cos θ
- cotθ = cos θ / sin θ
Reciprocal Identities
- sinθ = 1/cosecθ
- cosecθ = 1/sinθ
- cosθ = 1/secθ
- secθ = 1/cosθ
- tanθ = 1/cotθ
- cotθ = 1/tanθ
Pythagorean Identities
- sin2θ + cos2θ = 1
- 1 + tan2θ = sec2θ
- 1 + cot2θ = cosec2θ
Even and Odd Angle Formulas
- sin(-θ) = -sinθ
- cos(-θ) = cosθ
- tan(-θ) = -tanθ
- cot(-θ) = -cotθ
- sec(-θ) = secθ
- cosec(-θ) = -cosecθ
Co-function Formulas
- sin(900-θ) = cosθ
- cos(900-θ) = sinθ
- tan(900-θ) = cotθ
- cot(900-θ) = tanθ
- sec(900-θ) = cosecθ
- cosec(900-θ) = secθ
Double Angle Formulas
- sin2θ = 2 sinθ cosθ
- cos2θ = 1 – 2sin2θ
- tan2θ = 2 tanθ / 1-tan2θ
Half Angle Formulas
- sinθ = ±√1-cos2θ/2
- cosθ = ±√1+cos2θ/2
- tanθ = ±√1+cos2θ/1-cos2θ
Thrice of Angle Formulas
- sin3θ = 3sinθ – 4 sin3θ
- Cos 3θ = 4cos3θ – 3 cosθ
- Tan 3θ = 3tanθ – tan3θ/ 1- 3tan2θ
- Cot 3θ = cot3θ – 3cotθ/3cot2θ – 1
Product to Sum Formulas
- Sin A Sin B = 1/2 [Cos (A-B) – Cos (A+B)]
- Cos A Cos B = 1/2 [Cos (A-B) + Cos (A+B)]
- Sin A Cos B = 1/2 [Sin (A+B) + Sin (A-B)]
- Cos A Sin B = 1/2 [Sin (A+B) – Sin (A-B)]
Sum to Product Formulas
- Sin A + Sin B = 2 sin (A+B)/2 cos (A-B)/2
- Sin A – Sin B = 2 sin (A+B)/2 sin (A-B)/2
- Cos A + Cos B = 2 cos (A+B)/2 cos (A-B)/2
- Cos A – Cos B = 2 cos (A+B)/2 cos (A-B)/2
Trigonometry table
The table below contains trigonometric formulas for angles that are often utilised in problem solving.
| Degrees | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Radians | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| Sin θ | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| Cos θ | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| Tan θ | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| Cot θ | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| Sec θ | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
| Cosec θ | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
Inverse Trigonometric Functions
If Sin θ = x, then θ = sin-1 x = arcsin(x)
Similarly,
- θ = cos-1x = arccos(x)
- θ = tan-1 x = arctan(x)
Also, the inverse properties could be defined as;
- sin-1(sin θ) = θ
- cos-1(cos θ) = θ
- tan-1(tan θ) = θ
Signs of Trigonometric Ratios
- All Six trigonometric ratios are positive in the first quadrant
- Only are positive and the remaining all are negative in the second quadrant.
- Only are positive and the remaining all are negative in the third quadrant.
- Only are positive and the remaining all are negative in the fourth quadrant.
FAQs on Trigonometric Formulas
What is the basic formula for trigonometry
The basic formula in trigonometry relates the angles and sides of a right-angled triangle, such as sine, cosine, and tangent.
What are the 7 formula of trigonometry?
There are 7 fundamental trigonometric formulas, including sine, cosine, tangent, cosecant, secant, cotangent, and the Pythagorean theorem.
What is 15 trigonometry formula?
There is no standard 15 trigonometry formula. The core trigonometric formulas are usually limited to the fundamental 7.
What is the trigonometry formula for Class 11?
Trigonometry formulas for Class 11 cover the basics, including sine, cosine, tangent, and their inverses, as well as trigonometric identities.
Who is the father of trigonometry?
The father of trigonometry is considered to be Hipparchus.
Who is the mother of trigonometry?
There isn't a widely recognized mother of trigonometry as it is a collective field of mathematics.
What is theta angle?
Theta (θ) is a symbol used in trigonometry to represent an angle.
What are the 4 types of trigonometry?
The four main types of trigonometry are plane trigonometry, spherical trigonometry, hyperbolic trigonometry, and analytic trigonometry.









