Table of Contents
Introduction:
The center of mass of an object or a system of objects is a place defined relative to that object. The center of Mass is the average position of all pieces that are valued according to their Masses in a system. The Centroid is the location of the center of Mass for simple rigid objects with homogeneous density. It is possible that an object’s Center of Mass does not always lie above it. The Center of Mass of a uniform disc would be on its center, but the Center of Mass of a ring would be on its center but without any material. For intricate designs, the center of mass can be defined as the one point at which the total of the weighted position vectors of all parts equals zero.
A brief outline:
The Importance of the Mass Center:
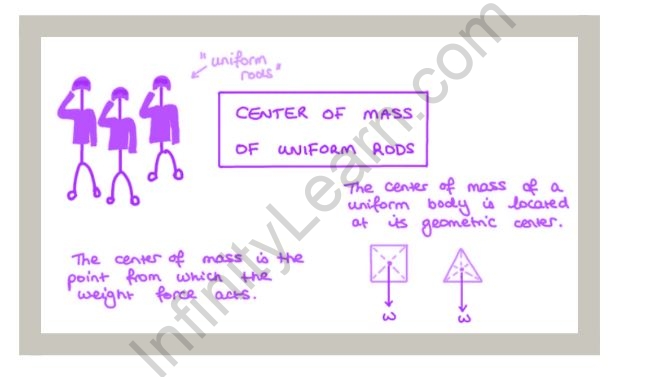
A system’s center of mass is the point at which any uniform force is applied to the object. Finding the Center of Mass of items is significant because it makes it easier to solve Mechanics problems and describe the motion of intricate and weirdly shaped objects. We assume that all of the Mass of an oddly-shaped object is focused in a tiny object positioned at the center of Mass while completing calculations, and this little thing is known as the point Mass.
Gravity’s Center:
The center of gravity of such a system is the imaginary point through which the force of gravity acts on an object or a system. When working on mechanical problems, it’s common to assume that the gravitational field is uniform, meaning that the Center of Gravity and the Center of Mass are in the same place.
Important concepts:
Take a rod with a mass of M and a length of L.
The mass of the rod per unit length is calculated as follows:
M/L = s
Make d x a little portion of the rod.
As a result, d m=M d x/L.
The integral of x d m divided by the integral of m will equal the center of mass.
where an x limit is a number between 0 and L.
center of mass is given as 1/L [x 2/2] L 0
If solved, we get center of mass = L/2
As a result, the center of mass of a uniform rod of mass M and length L is located in the rod’s midway point. Even the rod’s center of gravity is located in the middle. To put it another way, the rod’s entire weight is distributed across its middle point.
A uniform Rod’s Center of Mass:
When the location of the center of mass of a distribution of particles is required, the distribution of particles is frequently the set of particles that make up a rigid body. Because it only extends in one dimension, the uniform rod is the simplest rigid body for which to compute the center of mass. We’ll talk about an ideal uniform rod here. A physical uniform rod must have a diameter that is not zero. However, as long as the diameter of the rod is modest in comparison to its length, the ideal uniform rod is a fair approximation to the physical uniform rod.
Calculating the position of the center of mass is simple in the most basic scenario. A homogeneous thin rod is the simplest instance. A uniform thin rod is one in which the linear mass density, or mass per length of the rod, is the same at all points along its length. A uniform rod’s center of mass is located in the middle of the rod. The center of mass of a uniform rod extending along the x-axis from x=0 to x=L, for example, is at (L/2, 0).
When the context is obvious, the linear mass density, also known as linear density, is a measure of how effectively packed the constituent particles that make up the rod are. where the density is linear.
Visualize a uniform rod constructed of a lead-aluminum alloy with a non-uniform linear density as a function of the location to understand what a non-uniform rod is. Consider that the proportion of lead in the rod ranges smoothly from 0% at one end to 100% at the other. The linear density of this rod would be determined by its location along its length. A one-millimeter rod segment in one position will have a different mass than a one-millimeter rod segment in a different position.
Significance of center of mass of uniform rod in NEET exam:
The idea of the focal point of mass in the uniform bar is valuable in issues including a slender pole. To fathom rotational movement, the focal point of mass assumes an imperative part.
The basic inquiries on the focal point of mass in the uniform bar will assist you with planning for the following NEET tests. The NEET Crucial Problems were made by qualified instructors to help understudies who are deprived to guarantee that they are equipped for noting all material science focal points of mass inquiries.
Different inquiries on the focal point of mass in a uniform bar have been painstakingly produced for understudies of different sorts; understudies can download section-by-part basic inquiries in PDF design from the unending learn site and use them for additional investigations. Understudies ought to likewise study over the CBSE board’s Physics prospectus mindfully and download inquiries concerning the focal point of mass in an unbending body. This will extraordinarily help everybody in recognizing any blemishes in how they might interpret the standards.
FAQs (Frequently asked questions):
What is the uniform rod's center of mass?
A uniform rod's center of mass is located in the middle of the rod. A uniform rod's center of gravity is also located in the middle of the rod.
What is the rigid body's center of mass?
It's the location in or around an object where the object's entire mass can be considered concentrated. If the object is a solid symmetrical homogeneous object, such as a solid sphere or cube, the center of mass is inside it. Its geometrical center is where its center of mass is.
Is it required for there to be mass at the system's center of mass?
No, there does not have to be any mass at the system's center of mass. A ring's center of mass, for example, is at its center, where there would be no mass.





