Table of Contents
Introduction
Lawrence Joseph Henderson, one of the best scientists of the day, devised an equation in 1908 to compute the Hydrogen concentration in a buffer solution. Lawrence’s derivation is still extensively used today to compute the PH of a certain buffer solution. When a little amount of acid or base is added, or when the solution is diluted with pure solvent, a buffer is typically characterized as a solution that resists changes in pH. This characteristic is highly beneficial in keeping the pH of a chemical system at an optimal level so that reaction kinetics and equilibrium processes can be appropriately influenced.
A brief outline
A buffer solution is made up of either a weak acid and its conjugate base, or a weak base as well as its conjugate acid. “Salts” is a term used to describe conjugated forms. The Henderson Hasselbalch formula is a rough formula that demonstrates the relationship between a solution’s pH or pOH, the pKa or pKb, and the ratio of dissociated chemical species concentrations. The acid dissociation constant must be specified in order to utilize the equation. Unfortunately, most doctors are unaware of the equation’s limitations: it has several flaws and is much more descriptive rather than mechanistic. The Henderson-Hasselbalch equation has shown to be extremely useful in the study of mammalian acid-base physiology and is frequently employed in the treatment of acid-base disorders.
Important concepts
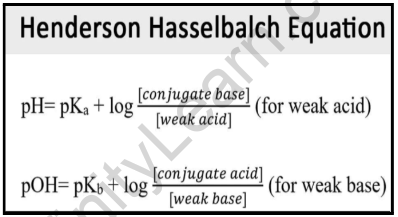
Henderson-Hasselbalch equation:
The Henderson-Hasselbalch equation can be written like:
pH = pKa + log10 ([A–]/[HA])
Where [A−] signifies the conjugate base (of the acid) molar concentration and [HA] denotes the weak acid molar concentration. As a result, the Henderson-Hasselbalch equation could also be written as:
pH = pKa + log [(Conjugate base/ Acid)]
American scientist Lawrence Joseph Henderson was the first to develop an equation that could compute the pH value of a given buffer solution. Karl Albert Hasselbalch, a Danish scientist, re-expressed this formula in logarithmic forms. The Henderson-Hasselbalch Equation was created as a result.
Derivation of Henderson-Hasselbalch Equation
Direct methods can be used to calculate the ionization constants of strong acids and strong bases. However, because the extent of ionization of weak acids and bases is very limited, the same procedures cannot be employed with them (weak acids and bases hardly ionize). As a result, the Henderson-Hasselbalch Equation is used to approximate the pH of various types of solutions.
Let us take the case of ionization of weak acid HA:
HA + H2O ⇋ H+ + A−
Acid dissociation constant, Ka can be assumed as:
Ka = [H+] [A−]/ [HA]
Taking, negative log of Right- and left-hand side
−log Ka = −log [H+] [A−]/ [HA]
⇒
−log Ka = −log [H+] – log [A−]/ [HA]
Thus,
−log [H+] = pH and – log Ka = pKa
The above equation becomes,
Ka = pH – log [A−]/ [HA]
By rearranging we get,
pH = pKa + log [A−]/ [HA]
Henderson-Hasselbalch equation, often known as Henderson equation, is the above equation. It’s great for calculating the pH of a buffer solution and determining the pH of equilibrium in acid-base reactions. We can deduce this when using the equation. pH = pKa
log [A−]/ [HA] = 0
[A−] = [HA]
That is, when pH = pKa, the concentration of both the species are the same, or, the acid will be half dissociated.
Correspondingly, for a weak base B:
B+H2O⇋OH−+HB+
Base dissociation constant, Kb, of the base can be specified as,
Kb = [BH+][OH−]/[B]
Putting the negative log of RHS and LHS
−logKb = −log [BH+] [OH−]/[B]
⇒−logKb⇒ −log [OH−]−log [BH+]/[B]
As we know,
−log [OH–] = pOH and −logKb = pKb
The above equation can be written as,
pKb = pOH − log [BH+]/[B]
Rearranging the equation,
⇒pOH = pKb +log [BH+]/[B]
Remember these key points:
- The value of [A]/[HA] becomes 1 when exactly half of the acid dissociates, meaning that the acid’s pKa is equivalent to the pH of the solution at this moment. (pH = log10(1) + pKa = pKa)
- The ratio of the linked acid to the dissociated acid changes tenfold for every unit change in the pH to pKa ratio. When the acid’s pKa is 7 and the pH of the solution is 6, the value of [A–]/[HA] is 0.1, but when the pH of the solution drops to 5, the value of [A–]/[HA] drops to 0.01.
- The value of [A–]/[HA] is determined by the pH and pKa values.
The Henderson-Hasselbalch Equation’s Limitations:
Because it implies that the concentrations of the acid and its conjugate base at equilibrium state will remain the same as that of formal concentration, the Henderson-Hasselbalch equation fails to predict appropriate results for strong acids and strong bases (the binding of protons to the base is neglected). The Henderson-Hasselbalch equation fails to provide accurate pH readings for highly dilute buffer solutions because it ignores water’s self-dissociation.
Significance of Henderson equation in NEET exam
The NEET test answers from Infinity Learn include general clarifications for the subjects. After great deliberation and effort, well-informed authorities respond. The PDF layouts will aid you in fully comprehending the section. Specialists devised the plans, which are presented in an exceptionally clear and accurate manner so that you can quickly embrace the concepts.
The rationale and computation are broken down into steps to help you see each component of the process. It will assist understudies in better comprehending the part and the concept of light occlusion, as well as the section’s principles as a whole. Understudies may be able to locate significant inquiries and corrective notes for NEET.
Also read: Heat Capacity and Specific Heat
FAQs
What do you mean when you say a solution's pH?
The pH of a solution is a measurement of the total number of H+ ions in the solution. This word is also useful in determining the acidity of a solution.
Why Does Buffer Solution Resist pH Changes?
When we add any acidic or basic component to a buffer solution, the pH does not change and it resists. Buffers include acidic components, such as HA, that neutralize OH- ions, as well as basic components, such as A-, that neutralize H+ ions. It will always maintain the pH of the solution by neutralizing little amounts of acid or base.
In terms of pharmaceutical analysis, how is the Henderson Hasselbalch equation used?
When estimating the pH levels in a buffer solution, this equation is crucial. In terms of pharmaceutical analysis, this mostly aids in the calculation of a molecule's PKA value using a chemical moiety. It's also useful for estimating the ratio of its ionized and unionized versions. This does, however, cover certain additional processes that are involved.