Stress-Strain Relationship

What is stress? What is strain? What is the relationship between stress-strain? In this article, we shall discuss everything related to stress, strain, their types, and also the stress-strain relationship.

What is Stress?

The term stress refers to forces per unit area within materials caused by externally applied forces, uneven heating, or permanent deformation. The definition of stress permits accurate description and prediction of elasticity, plasticity, and fluid behaviour.

Stress can be calculated as follows:

σ = FA

Where σ is the stress applied, F is the force applied and A is the area of the force application.

The unit of stress is N/m ²

Types of Stress:

There are several types of stress in physics, but they are generally divided into three categories: Normal stress, Tangential stress or shearing stress, and Hydraulic stress.

Normal Stress:

A normal force is what occurs when a member is loaded by an axial force.In other words, when the force is applied perpendicularly to the body it is called normal stress.

Longitudinal Stress:

When the length of the body changes due to normal stress applied, it is called longitudinal stress.

Bulk Stress or Volume Stress:

Volume stress refers to the change in volume of the body that occurs as a result of the stress.

As the body is stressed normally, volume or length changes, and as the body is stressed tangentially, volume changes.

Tensile Stress:

Force per unit area is the definition of tensile stress. Due to the force, the length of the body increases when the stress is applied.

Compression Stress:

Changing the shape and volume of the body is caused by an application of tangential force. When the compression stress has been applied the length of the body is decreased

What is Strain?

In physics, strain is the amount of deformation that occurs in a body as a result of a force applied, divided by the initial dimensions of the body.

According to the following equation, a solid’s deformation is proportional to its length:

Є = δlL

Where Є is the strain due to stress applied, δl is the change in length and L is the original length of the material.

As the strain only describes the relative change in shape, it is dimensionless.

Types of Strain:

There are three types of strains:

• Normal strain or longitudinal strain: Normal strain is the ratio of the change in length of a body with respect to its original length. It is also known as longitudinal strain since it is concerned with the change in length of the body in relation to its original length. Mathematics represents longitudinal strain as follows:

S ₁ =△V /V

• Shearing strain is defined as the angular distortion made by the body, so it is equal to the displacement of the body surface in relation to the body height, but keep in mind that the body surface is the one that bears the strain. The following mathematical expression can be used to express it:

S ₂ =l /H

• Volumetric strain, or bulk strain: The volumetric strain ratio is the volume change of a body compared to its original volume. It is also known as bulk strain because it takes into account the body’s entire volume. In mathematics, this is expressed as follows:

 

S ₁ =△V /V

Stress-Strain Curve:

Information regarding elastic properties is the most important when studying solids and their mechanical properties. By studying the stress-strain relationships, we can learn about the elastic properties of materials.

The stress-strain curve of the material gives its stress-strain relationship. Stress and strain values are plotted on a stress-strain curve. The following example illustrates how a stress-strain curve is plotted.

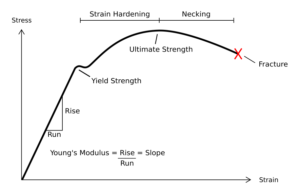
Stress-Strain Relationship Graph:

Stress-strain diagrams have the following regions:

(i) Proportional Limit: Hooke’s Law describes the region in the stress-strain curve that obeys it. A proportionality constant known as Young’s modulus is derived from the stress-strain ratio at this limit. The region OA in the above graph represents the proportional limit.

(ii) Elastic Limit: This is the point in the graph at which the material returns to its original position after the load acting on it has been removed. Beyond this point, the material does not return to its original position, and plastic deformation can be seen.

(iii) Yield Point: The yield point is defined as the point where the material starts to deform plastically. If the yield point is exceeded, the material becomes permanently deformed. Two yield points can be identified (i) upper yield point and (ii) lower yield point.

(iv) Ultimate Stress Point: This point represents the maximum stress that the material can withstand before breaking.

Beyond this point, failure occurs.

(v) Fracture or Breaking Point: At this point in the stress-strain curve, the material fails.

What causes bones to fracture?

Tension or compression do not cause bones to shatter. In fact, they are typically broken by bending or sideways stress, resulting in snapping or shearing of the bone. The behaviour of bones in tension and compression has an enormous impact on how much weight they can support. Structural components that bear weight, such as columns in buildings and trees, are considered bones.

Building columns contain steel-reinforcing rods, and fibrous trees and bones are examples of weight-bearing structures. A different bone serves a different purpose in the body and is subject to different forces depending on its location. Therefore, the top of the femur’s bone is made up of thin sheets separated by marrow, though the bones in other places may be cylindrical and filled with marrow or solid.

Also read: Here’s How to Boost Your Percentage in the Board

FAQs: Stress-Strain Relationship

What does the stress-strain curve show?

A stress-strain curve is a graphical representation of how a material will react when loaded. It shows a comparison between stress and strain experienced by the object

What is the relation between stress and strain?

Up to a certain elastic limit, strain and stress are proportional. Hooke's law explains this relationship. According to Hooke’s law, the strain in a solid is proportional to the applied stress.

What is the ratio between stress and strain?

When the force is applied to the body, its resistance to being deformed elastically, which means not permanently, is calculated by the ratio of stress to the strain. This ratio is called elastic modulus or modulus of elasticity.

Is pressure the same as stress?

The difference between stress and pressure is the fact that with pressure the force is external, while in stress the force is internal, so it cannot change its shape or size.