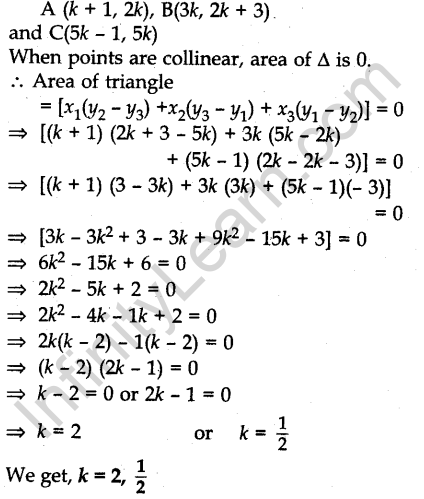Table of Contents
Time allowed: 3 hours Maximum marks: 90
GENERAL INSTRUCTIONS:
- All questions are compulsory.
- The Question Taper consists of 31 questions divided into four Sections A, B. C. and D.
- Section A contains 4 questions of 1 mark each. Section B contains 6 questions of 2 marks each, Section C contains 10 questions of 3 marks each and Section D contains 11 questions of 4 marks each.
- Use of calculators is not permitted.
SET I
SECTION A
Questions number 1 to 4 carry 1 mark each
Question.1. If the quadratic equation px2– 2-√5 px + 15 = 0 has two equal roots, then find the value of p.
Answer.

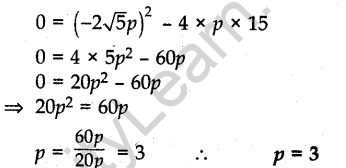
Question.2. In Figure 1, a tower AB is 20 m high and BC, its shadow on the ground, is 20-√3 m long. Find the Sun’s altitude.

Answer.
![]()

Question.3. Two different dices are tossed together. Find the probability that the product of the two numbers on the top of the dice is 6.
Answer.
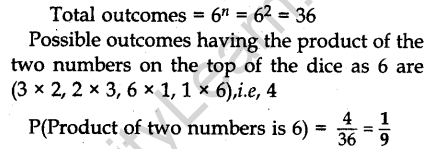
Question.4. In Figure 2, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.
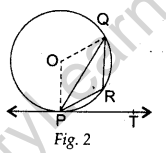
Answer.

SECTION B
Questions number 5 to 10 carry 2 marks each.
Question.5. In Figure 3, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120°, then prove that OR = PR + RQ.
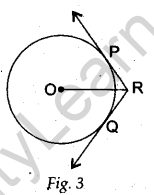
Answer.


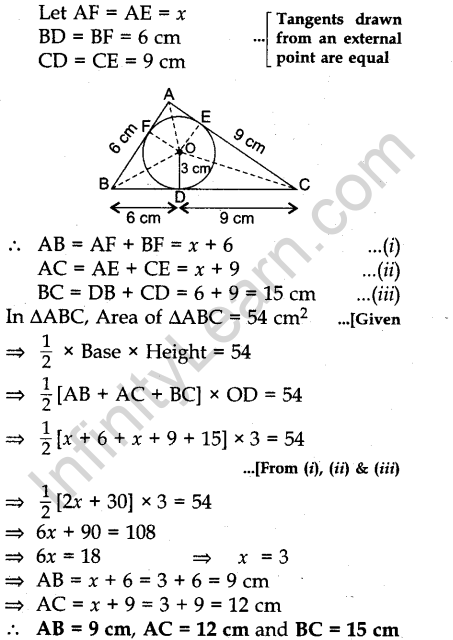
Question.6. In Figure 4, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ∆ABC is 54 cm2, then find the lengths of sides AB and AC.

Answer.
Question.7. Solve the following quadratic equation for x:
![]()
Answer.
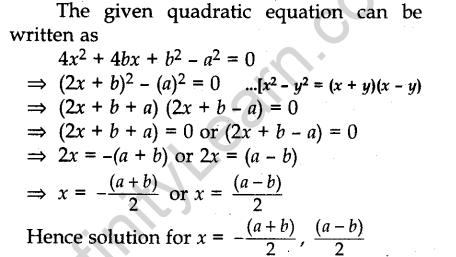
Question.8. In an AP, if S5+ S7 = 167 and S10 = 235, then find the AP, where Sn denotes the sum of its first n terms.
Answer.
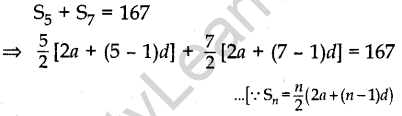
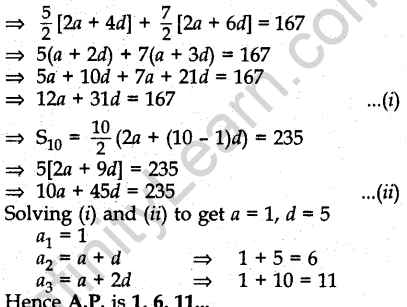
Question.9. The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right triangle, right-angled at B. Find the value of p.
Answer.

Question.10. Find the relation between x and y if the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
Answer.
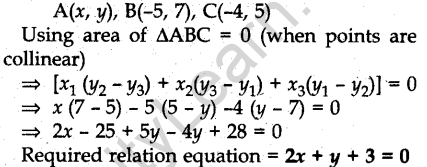
SECTION C
Questions number 11 to 20 carry 3 marks each.
Question.11. The 14th term of an AP is twice its 8th term. If its 6th term is -8, then find the sum of its first 20 terms.
Answer.

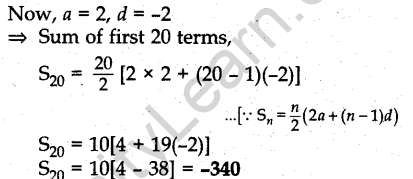
Question.12. Solve for x:
![]()
Answer.

Question.13. The angle of elevation of an aeroplane from a point A on the ground is 60°. After a flight of 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a constant height of 1500 √3 m, find the speed of the plane in km/hr.
Answer.

Question.14. If the coordinates of points A and B are (-2, -2) and (2, -4) respectively, find the coordinates of P such that AP = 3/5 AB, where P lies on the line segment AB.
Answer.

Question.15. The probability of selecting a red ball at random from a jar that contains only red, blue and orange balls is 1/4. The probability of selecting a blue ball at random from the same jar is 1/3 . If the jar contains 10 orange balls, find the total number of balls in the jar.
Answer.

Question.16. Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60°. Also find the area of the corresponding major segment. [Use π = 22/7 ]
Answer.

Question.17. Due to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and offered to contribute 50% of the cost. If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m with the conical upper part of same diameter but of height 2.8 m, and the canvas to be used costs Rs 100 per sq. m, find the amount, the associations will have to pay. [Use π = 22/7 ] What values are shown by these associations?
Answer.


Values: Helping the flood victims and showing concern for humanity.
Question.18. A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of the each bottle, if 10% liquid is wasted in this transfer.
Answer.

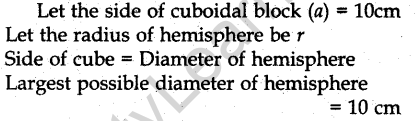
Question.19. A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs 5 per 100 sq. cm. [Use π= 3.14]
Answer.

Question.20. 504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area. [Use π = 22/7 ]
Answer.

SECTION D
Questions number 21 to 31 carry 4 marks each.
Question.21. The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
Answer.


Question.22. Find the 60th term of the AP 8,10,12,…, if it has a total of 60 terms and hence find the sum of its last 10 terms.
Answer.
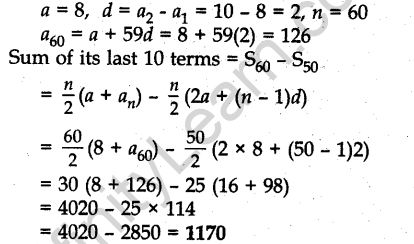
Question.23. A train travels at a certain average speed for a distance of 54 km and then travels a . distance of 63 km at an average speed of 6 km/h more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
Answer.

Question.24. Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Answer. See Q. 27,2012 (I Outside Delhi).
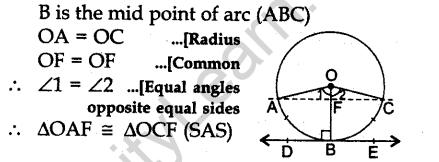
Question.25. Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Answer.

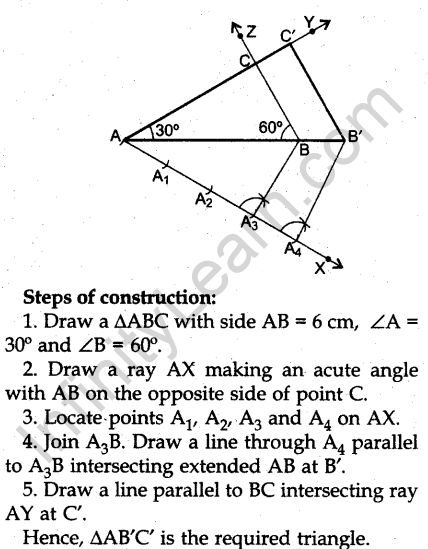
Question.26. Construct a ∆ABC in which AB = 6 cm, ∠A = 30° and ∠B = 60°. Construct another ∆AB’C’ similar to ∆ABC with base AB’ = 8 cm.
Answer.
Question.27. At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30°. The angle of depression of the reflection of the cloud in the lake, at A is 60°. Find the distance of the cloud from A.
Answer.


Question.28. A card is drawn at random from a well-shuffled deck of playing cards. Find the probability that the card drawn is
(i) a card of spade or an ace. (ii) a black king.
(iii) neither a jack nor a king. (iv) either a king or a queen.
Answer.

Question.29. Find the values of k so. that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units.
Answer.

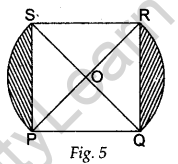
Question.30. In Figure 5, PQRS is a square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersection of its diagonals. Find the total area of the two flower beds (shaded parts).
Answer.


Question.31. From each end of a solid metal cylinder, metal was scooped out in hemispherical form of same diameter. The height of the cylinder is 10 cm and its base is of radius 4.2 cm. The rest of the cylinder is melted and converted into a cylindrical wire of 1.4 cm thickness. Find the length of the wire. [Use π = 22/7 ]
Answer.

SET II
Note: Except for the following questions, all the remaining questions have been asked in Set-I.
Question.10. If A(4, 3), B(-l, y) and C(3, 4) are the vertices of a right triangle ABC, right-angled at A, then find the value of y.
Answer.
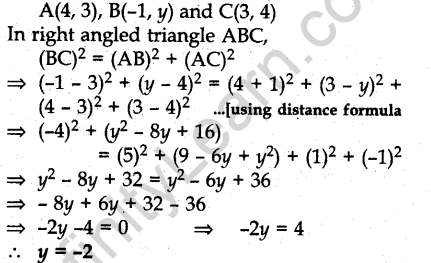
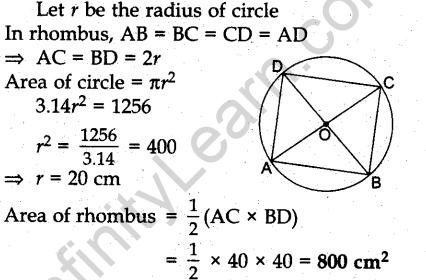
Question.18. All the vertices of a rhombus lie on a circle. Find the area of the rhombus, if the area of the circle is 1256 cm2. [Use π= 3.14]
Answer.
Question.19. Solve for x:
![]()
Answer.

Question.20. The 16th term of an AP is five times its third term. If its 10th term is 41, then find the sum of its first fifteen terms.
Answer.


Question.28. A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed.
Answer.

Question.29. Prove that the tangent at any point of a circle is perpendicular to the radius through the I point of contact.
Answer. See Q. 27, 2012 (I Delhi).
Question.30. Construct a right triangle ABC with AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD, the perpendicular from B on AC. Draw the circle through B, C and D and construct the tangents from A to this circle.
Answer. See Q. 13, 2014 (I Delhi).
Question.31. Find the values of k so that the area of the triangle with vertices (k + 1, 1), (4, -3) and (7, -k) is 6 sq. units.
Answer.
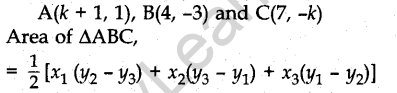
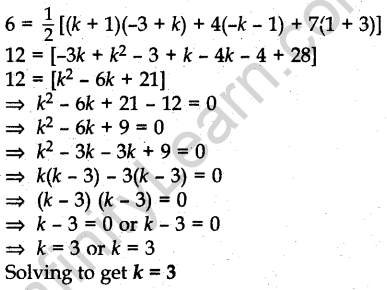
SET III
Note: Except for the following questions, all the remaining questions have been asked in Set-l.
Question.10. Solve the following quadratic equation for x:
![]()
Answer.
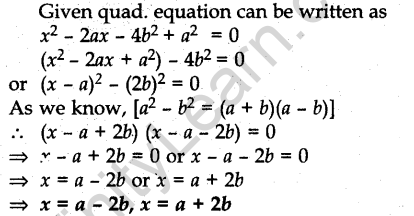
Question.18. The 13th term of an AP is four times its 3rd term. If its fifth term is 16, then find the sum of its first ten terms.
Answer.

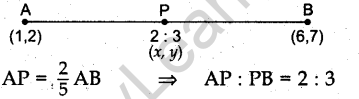
Question.19. Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) such that AP=2/5 AB.
Answer.

Question.20. A bag contains, white, black and red balls only. A ball is drawn at random from the bag. If the probability of getting a white ball is 3/10 and that of a black ball is 2/5, then find the probability of getting a red ball. If the bag contains 20 black balls, then find the total number of balls in the bag.
Answer.

Question.28. A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
Answer.

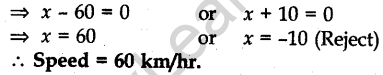
Question.29. An Arithmetic Progressions, 12,19,… has 50 terms. Find its last term. Hence find the sum of its last 15 terms.
Answer.

Question.30. Construct a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60°. Now construct another triangle whose sides are 5/7 times the corresponding sides of ∆ABC.
Answer. See Q. 18, 2011 (I Delhi).
Question.31. Find the values of k for which the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear.
Answer.