Bernoulli’s Theorem Derivation

The Principle of Bernoulli

Bernoulli’s equation determines the link between a flowing fluid’s pressure, elevation, and speed. This equation is based on energy conservation and conversion. It has been known as Bernoulli’s principle since Daniel Bernoulli proposed it. This technique can be used in various applications, including spray guns, venturi meters, and nozzles, among others. We can address many real-world engineering problems involving fluid flow by employing Bernoulli’s principle. Here we look at Bernoulli’s theorem derivation.

Equation of Continuity

When an incompressible and non-viscous liquid flows in a streamlined motion through a tube with a non-uniform cross-section, the product of the area of cross-section and the velocity of flow is the same at every point in the tube, according to the continuity equation.
As a result, A1v1=A2v2 Av= Constant v1A can be written.
The cross-sectional areas of the tube are A1 and A2. And their relative speeds are v1 and v2.

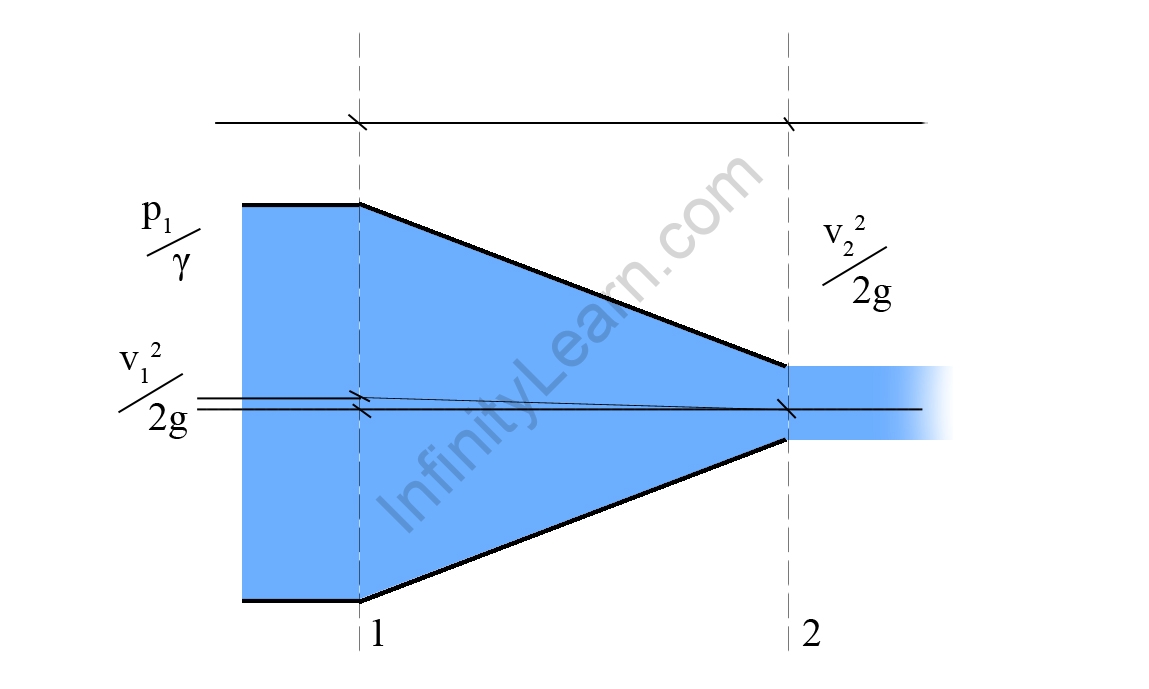
Bernoulli’s Equation

The following assumptions were used to get Bernoulli’s equation:

• The fluid must be perfect.
• It’s important to maintain a consistent flow.
• There should be no squandering of energy.
• Incompressible fluids should be used.
• Irrotational flow is preferred.

Significance of Bernoulli’s Theorem Derivation in the IIT JEE exam

It is critical to take a holistic approach to every facet of a subject’s chapter. It will adequately prepare you for the exam and clarify your understanding of each topic. It will help you in JEE preparation and answer conceptual problems in the exam.

Bernoulli’s Theorem Derivation

Consider a fluid traveling through a pipe with various cross-sectional areas in various regions and varying heights, as depicted in the diagram below. Take a look at the flow in two regions: BC and DE. Assume the fluid was initially located between B and D. The fluid would have traveled in an infinitesimal time interval (t). If v1 is the speed at B and v2 is the speed at D, the fluid at B has traveled v1t distance to C. The fluid begins at D and flows to E in the same interval t, covering a distance equal to v2t. Pressures P1 and P2 bond the two regions as illustrated on the plane face of areas A1 and A2.

W1=P1A1(v1t)=P1V is the work done on the fluid at the left end (BC).

Now, if the same volume V travels through both regions according to the continuity equation, the work done by the fluid at the other end (DE) is W2=P2A2(v2t)=P2V, or we can say the work done on the fluid is –P2V. W1–W2=(P1–P2)V is the overall work done on the fluid.
If the fluid density is, then m=A1v1t=V is the mass moving through the pipe in time t, and U=gV(h1–h2) is the change in gravitational potential energy.
And K=(12)V(v22–v21) is the change in kinetic energy.
After applying the work-energy theorem to this fluid volume, (P1–P2)V=(12)V(v22–v21)+gV(h2–h1) is obtained.

Now divide each term by V to get the following term: (P1–P2)=(12)(v22–v21)+g(h2–h1)
Now, if we rearrange the terms above, we get:
P1+(12)ρv21+ρgh1=P2+(12)ρv22+ρgh2

Bernoulli’s equation is this. Because 1 and 2 can refer to any two points along the pipeline, the phrase can be written as:
P+(12)
v2+gh

Where P is the static pressure of the fluid at the cross-section, d is the density of the flowing fluid, v is the mean velocity of the fluid flow at the cross-section, and his the elevation head of the cross-section from the datum, and g is the acceleration due to gravity.

FAQs

What do you mean when you say continuity equation?

When an incompressible and non-viscous liquid flows in a streamlined motion through a tube with a non-uniform cross-section, the product of the area of cross-section and the velocity of flow is the same at every point in the tube, according to the continuity equation.

In fluid mechanics, what is Bernoulli's theorem?

In fluid dynamics, Bernoulli's theorem is the relationship between pressure, velocity, and elevation in a moving fluid (liquid or gas) with negligible compressibility and viscosity (internal friction) and a steady, or laminar flow.

Infinity Learn App

Now you can find answers to all your subject queries & prepare for your Exams on our Ultimate Learning App for Classes 6 to 12 – Infinity Learn.