Important Topic of Physics: Toppling

Toppling: The greatest angle to which you may tip anything before it returns to its original form is a basic and practical measure of stability. Even if you merely tilt the thing a little bit, the object will return to its original position due to the force of gravity pulling on it. However, gravity takes over and moves it to a new place if you tilt the object beyond a certain angle. The thing will now fall onto its side rather than back onto its base.

Condition of toppling

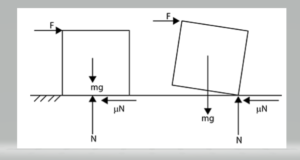
The instantaneous axis of rotation moves when a torque is applied to a body resisting change of motion (typically due to friction) (usually due to shifting of normal). If the instantaneous axis of rotation slips outside the body, the body topples. This is depicted in the diagram attached.

The greatest angle to which you may tip anything before it returns to its original form is a basic and practical measure of stability. Even if you merely tilt the thing a little bit, the object will return to its original position due to the force of gravity pulling on it. However, gravity takes over and moves it to a new place if you tilt the object beyond a certain angle. The thing will now fall onto its side rather than back onto its base.

Example – A cubical block with mass m and side L lies on a rough horizontal surface with friction coefficient. The diagram illustrates that a horizontal force F is imparted to the block. Find the least force necessary to collapse the block if the coefficient of friction is high enough that it does not slide before falling. ​

Solution:
In situation 1, when the least amount of force is used,
$F=\mu N$
$N=mg$
$\therefore F=\mu mg$
Now,
Block topples when force surpasses a certain threshold.
Taking a moment about the toppling axis,
$\sum M=0$ ……………. Still in equilibrium
$\therefore \sum M=\sum F.d$
⇒0=F×L−mg×2L​
∴F=2mg

Centre of mass

Things are stable if their center of mass (through which the force of gravity pressing on the item operates) is inside their footprint, which is a helpful way of looking at this subject.

The object topples when an item is tilted, and the force of gravity’s action path goes outside its footprint.

As a result, an object’s centre of mass is linked to the turning effect of forces.

​Attempt to push a book over a smooth table without it spinning. Did you manage to complete the task? Then you’re pointing at the mass center. Push along an edge at a right angle to the first one once more. If you can pull off another successful pointing act, the book’s center of mass will be on the line where these two cross. Because the book is three-dimensional, you’ll need to perform a measurement along the third axis to determine where the point that represents the center of mass is located along the line.

For the book, the centre of mass is a unique location. You worked with pressures acting in one direction only before in this topic. This line must travel through the centre of mass if the item moves without spinning due to the forces. When we reduce the world to forces acting on point particles, the points must represent the objects’ centre of mass.

Discussion

A limit equilibrium analytical solution for block toppling failure is proposed and tested using a shaking table model of an anti-dip rock slope. The theoretical conclusions, including the block deformation characteristics and overall slope stability requirement, are able to match the experimental observations well. Some assumptions are simplified in the offered analytical analysis, such as the block widths being the same, the strength parameters being the same for every block, and the failure base being a linear shape. It is well recognised that real-world slopes are frequently significantly more complex than the idealised slope mode. If that’s the case, the engineering geological generalisation technique should be used to abstract the control elements and arrive at a simplified but representative engineering geological model.

Conclusions

A limit equilibrium solution for block toppling failure is provided in this paper. In the analytical solution, the seismic loads and connectivity of the block base joint are taken into account. The shake table test is then applied to an anti-dip rock slope model. It demonstrates that the theoretical solutions can handle most of the deformation aspects seen during the shaking table test when the incoming wave increases, such as modes, deformation block positions, and overall FOS. The provided analytical solution may be inferred to be a universal technique for estimating the block toppling deformation characteristics and stability of anti-layered rock slopes with a non-persistent or persistent block base joint under static or seismic conditions.

FAQs

What is a support base?

The portion of the ground surface with which the body makes contact is known as the base of support (BOS). The centre of gravity (COG) is the point at which the centre of mass (COM) intersects the BOS perpendicularly. The COG is positioned within the BOS in a stable posture.

In physics, what does it mean to topple?

When two things interact with each other in physics, they are said to be linked. Coupling links two oscillating systems in classical mechanics, such as two pendulums connected by a spring. Both items' oscillatory patterns are affected by the link.

What is vehicle toppling?

In physics, the image result for Toppling is When taking a steep slope at high speed, there is always the risk of a car collapsing. As a result, they must slow down while approaching bends. Toppling is caused by a movement in the centre of gravity from its normal location.

What are the requirements for toppling?

Toppling condition. The instantaneous axis of rotation moves when a torque is applied to a body resisting change of motion (typically due to friction) (usually due to shifting of normal). If the instantaneous axis of rotation slips outside the body, the body topples.

Is toppling without friction possible?

The rod will only entirely tumble if the torque is significant enough to force the centre of mass first to reach and then spin over the contact pivot point, continually moving horizontally down the surface without friction.