Table of Contents
A Brief Outline
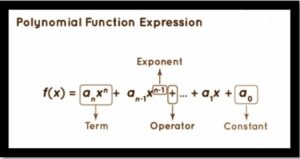
Polynomial functions are expressions with varied degrees of variables, coefficients, positive exponents, and constants. The highest power of the variable raised is the level of the polynomial function.
Important Concepts
Polynomial Function Types
The following are some examples of various types of polynomial functions based on their degrees:
- Constant Polynomial Function – A constant polynomial function is one whose value remains constant across time. It does not change and does not include variables.
- Linear polynomial functions have a degree of one and are known as zero polynomial functions.
- Linear Polynomial Function – Linear polynomial functions are polynomial functions having a degree of one.
- Quadratic Polynomial Function – Quadratic polynomial functions are polynomial functions having a degree of two.
- Cubic Polynomial Function – Cubic polynomial functions are polynomial functions having a degree of three.
- Quartic Polynomial Function – Polynomial functions having a degree of four are referred to as quartic polynomial functions.
Some of the instances of polynomial functions are specified beneath:
2x² + 9x +8 = 0
7x -5 = 3
4x³ + x² -5 = 0
Because all of the variables in the above equation possess positive integer exponents, all three equations are polynomial functions. Some of the following expressions are not called polynomial equations since the polynomial does not include negative integer exponents, fraction exponents, or division.
4x-1 + 1= 0
5×1/2 +2x + 1
(8x +1) /1
Significance of polynomial functions in IIT JEE exam
A polynomial function is a mathematical function that can be expressed as a sum of terms, each of which is a product of a real number and a power of x. Polynomial functions are important in the IIT JEE exam as they are used to model a wide variety of real-world situations. In many cases, polynomial functions can be used to approximate the behavior of more complex mathematical functions.
One of the most important applications of polynomial functions in the IIT JEE exam is in the solution of equations. Polynomial functions can be used to solve equations of the form ax^2 + bx + c = 0, where a, b, and c are real numbers. In many cases, the polynomial function can be factored into a product of two simpler polynomial functions. This factoring can often be used to find the roots of the equation, or the points at which the equation is equal to zero.
Polynomial functions are also important in the analysis of data. In many cases, a data set can be best described by a polynomial function. This function can be used to model the trend of the data set and to make predictions about future values. Polynomial functions can also be used to find the maximum and minimum values of a data set.
FAQs
The equations generated using variables, exponents, and coefficients are known as polynomial equations. The greater the number of unique components of the equation, the higher the degree of exponents. Polynomial Equations can be solved by considering the degree and variables in the equation.
The maximum power of the variable in an algebraic statement is the degree of a polynomial in a single variable. To put it another way. The biggest or greatest exponent of a polynomial for a single variable, such as x, is called the degree.
These functions are used to represent algebraic expressions that meet particular criteria. They are also capable of performing a wide range of tasks. What are polynomial equations and how do you explain them?
Explain what a polynomial's degree is?
What is a polynomial function's purpose?



