Ampere’s Law

Just as the electric field in space is proportional to the charge that serves as its source, the magnetic field in space around an electric current is proportional to the electric current that serves as its source. According to Ampere’s Law, the sum of the length elements times the magnetic field in the direction of the length element equals the permeability times the electric current confined in the loop for any closed-loop path. In the case of electric fields, Gauss’s Law, which is a hugely helpful tool for estimating electric fields, quantifies the relationship between field and source.

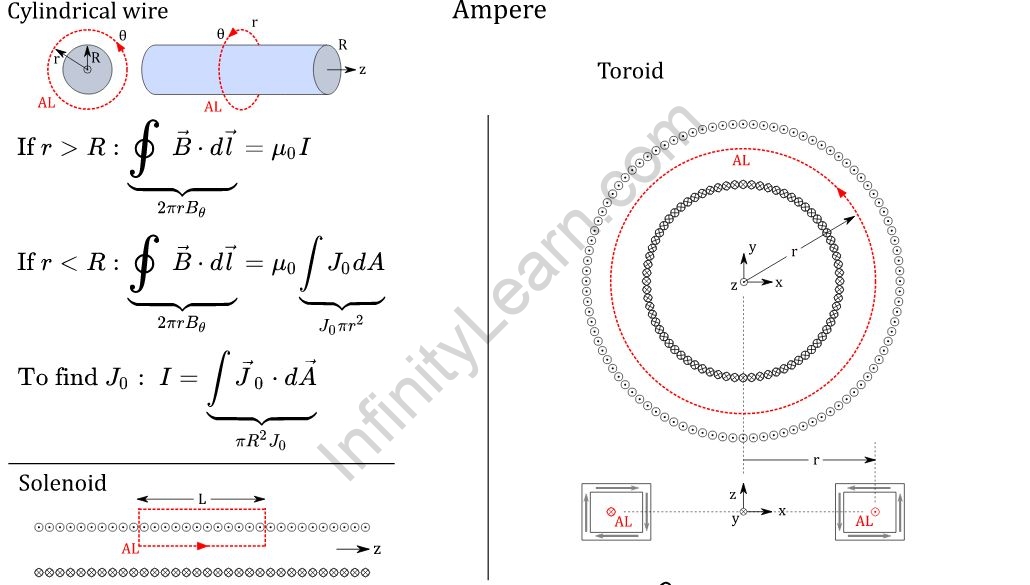
The Magnetic Induction due to a long amperes wire, defining the Magnetic field inside a toroid, assessing the Magnetic field created by a long current-carrying conducting cylinder, and evaluating the Magnetic field inside the conductor is just a few of the many applications of Ampere’s Law in real life. Among the most common practical uses of Ampere’s circuital Law are motors, generators, and transformers, to name a few. As a result, we can conclude that this is a crucial component of the student’s conceptual comprehension.Since its creation, Ampere’s Law has acquired popularity due to its practicality. It is often used in real-life settings. The production of machines is among the most well-known venues where Ampere’s Law is often utilized.

A brief outline

• One of the most important laws of electromagnetism is Ampere’s Law. Discovering the interpretation for any closed-loop path is what this is all about.
• It asserts that the permeability times the electric current is equal to the sum of the length elements times the magnetism in the direction of the length element.
• This law helps us to keep a proper bridge between electric and magnetic fields in place. It also shows how magnetic fields and pulsed electrical are related mathematically.
• The magnetic field created by an electric current flowing through a wire of any shape can be calculated using Amperes’ law.
• Ampere’s law is a useful law that connects the net magnetic field along this closed loop to the electric current that flows through it.
• André-Marie Ampère found it in the year 1826. Ampere’s law is an expression describing the relationship between the magnetic field and the current that produces it.

Important concepts

The line integral of the magnetic field around any arbitrary path is proportional to the net electric current contained by that channel, according to the definition. Furthermore, Maxwell generalized this law to include magnetic fields that emerge from sources other than current. As a result, one of four Maxwell equations is Ampere law.

The law’s integral form is as follows:

∮Bds=μ0I

Where ‘I’ is current and ‘0’ is the permeability of free space.

In addition, in the form of a summary:

\sumBΔS=μ0I

Ampere’s law concept

Ampère’s Law requires that all currents be constant. As a result, the present does not alter across time. Also, only currents passing the path’s interior must be included, as they will contribute to the magnetic field in some way. Currents must be interpreted in terms of their algebraic signs. To discern its directions and signals, one can apply the right hand’s rule. If the magnetic field is normal to the given route at any point, the total magnetic circulation will be zero. When computing the magnetic fields of current distributions with a high degree of symmetry, Ampère’s Law will come in handy.

Ampere’s Law Applications

Ampere’s law has a wide range of applications. Its primary use is to calculate the magnetic field produced by an electric current. Electromagnets, motors, generators, transformers, and other devices can benefit from this. Ampere’s law simplifies many calculations by employing a specific symmetry.

The following is a list of instances in which Ampere’s circuital law is used.

• Solenoid
• The wire that is straight
• The wire that is thick
• Conductor in the shape of a cylinder
• solenoid with a toroidal shape

It’s worth mentioning that the operating idea of such a law is the same throughout each process, regardless of the fact that how it’s executed changes a lot. It is the basic working principle of many machines, and it is frequently seen as a part of other equipment.

Circuital Law of Ampere

The line integral of the magnetic field encircling a closed-loop equals the algebraic total of currents going through the loop, according to Ampere’s circuital equation. If a conductor is transporting current I, the flow of current forms a magnetic field around the wire. The left side of the equation states that if an ideal path encircles the wire and the magnetic field is applied at each point, the current surrounded by this path, as represented by Ienc, is numerically equivalent to the current encircled by this route.

Significance of Ampere’s law in NEET exam

Understudies can undoubtedly learn about Ampere’s Law by visiting the limitless site to advance free of charge. Understudies can utilize the site to take notes on an assortment of other significant thoughts. Limitlessness Learn accepts that training is for everybody, so it makes all of its review apparatuses accessible to understudies free of charge, so they can see them and save them for some time later. Test papers, exercise manuals, earlier year’s inquiry papers, and different assets are available to assist understudies with cementing their insight in anticipation of the NEET test.

FAQs (Frequently asked questions)

Question 1: What is the need for Ampere’s law equation?

Answer: According to Ampere’s law, the total of the elements of the component of the magnetic field for a closed channel equals the product of electric current and empty’s permeability.

Question 2: What is the objective of Ampere’s law?

Answer: While the symmetry of the situation allows, we can employ Ampere’s law in light of introductory Electromagnetic theory. When the magnetic field surrounding an ‘Amperian loop’ is constant, this is what it signifies.

Question 3: State Ampere’s circuital law?

Answer: “The integral magnetic field line around a closed-loop equals the bunch of times the algebraic summation of currents travelling through the loop,” says Ampere’s circuital law.