Table of Contents
Introduction
Kirchhoff’s circuit laws are two equalities in the lumped element model of electrical circuits that deal with a current and potential difference (commonly known as voltage). Gustav Kirchhoff, a German physicist, described them for the first time in 1845. This generalised Georg Ohm’s work and predated James Clerk Maxwell’s work. Kirchhoff’s rules, or simply Kirchhoff’s laws, are widely used in electrical engineering. These laws, which can be applied in time and frequency domains, serve as the foundation for network analysis.
In the low-frequency limit, both of Kirchhoff’s laws can be viewed as corollaries of Maxwell’s equations. They are accurate for direct current (DC) circuits and for alternating current (AC) circuits at frequencies where the wavelengths of electromagnetic radiation are very large in comparison to the circuits.
We saw in the Resistors tutorial that when two or more resistors are connected in series, parallel, or combinations of both, a single equivalent resistance (RT) can be found and that these circuits obey Ohm’s Law. However, in complex circuits such as bridge or T networks, we cannot always rely solely on Ohm’s Law to determine the voltages or currents circulating within the circuit.
For these types of calculations, we need rules that allow us to obtain the circuit equations, and we can use Kirchhoff’s Circuit Law to do so.
Overview
Gustav Kirchhoff, a German physicist, developed a pair of laws dealing with the conservation of current and energy within electrical circuits in 1845. Kirchhoff’s Voltage and Current Law are the names given to these two laws. These laws aid in calculating the electrical resistance of a complex network, or impedance in the case of alternating current, as well as the current flow in the network’s various streams. Kirchhoff’s Current Law is also known by the names Kirchhoff’s First Law and Kirchhoff’s Junction Rule. The Junction rule states that in a circuit, the sum of currents in a junction equals the sum of currents outside the junction. Kirchhoff’s Voltage Law is also known as Kirchhoff’s Second Law or Kirchhoff’s Loop Rule. The sum of the voltages around the closed loop is equal to null, according to the loop rule.
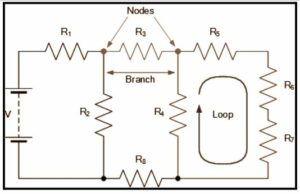
Kirchhoff’s Laws of current and voltage are central to circuit analysis. With these two laws, as well as the equations for individual components (resistor, capacitor, inductor), we have the fundamental toolset required to begin analysing circuits. Kirchhoff’s laws are crucial in the analysis of closed circuits. Consider the circuit depicted in the figure below, which consists of five resistors in a series and parallel configuration. It is impossible to reduce this circuit to a combination of series and parallel connections. Using Kirchhoff’s rules, however, one can analyse the circuit to determine the parameters of this circuit using the resistor values (R1, R2, R3, r1, and r2). It is also worth noting in this example that the values E1 and E2 represent voltage sources (e.g., batteries).
kirchhoff’s voltage law
The analysis of lumped parameter circuits is based on Kirchhoff’s current law and Kirchhoff’s voltage law. These laws, combined with the voltage-current characteristics of the system’s circuit elements, allow us to perform a systematic analysis of any electrical network. Kirchhoff’s voltage law is presented in this section. KVL is based on the concept of a loop. A loop is any closed path through the circuit that does not pass through the same node more than once. To make a loop, begin at any node in the circuit and trace a path through the circuit until you return to your original node.
Kirchhoff’s current law
Kirchhoff’s Circuit Principles define a set of basic network laws and theorems for the voltages and currents around a circuit, allowing us to solve complex circuit problems.
We saw in the Resistors tutorial that when two or more resistors are connected in series, parallel, or combinations of both, a single equivalent resistance (RT) can be found and that these circuits obey Ohm’s Law. However, in complex circuits such as bridge or T networks, we cannot always rely solely on Ohm’s Law to determine the voltages or currents circulating within the circuit. For these types of calculations, we need rules that allow us to obtain the circuit equations, and we can use Kirchhoff’s Circuit Law to do so.
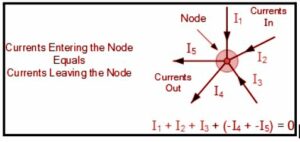
Kirchhoff’s Current Law, or KCL, states that the “total current or charge entering a junction or node is exactly equal to the charge leaving the node because it has no other place to go except out, as no charge is lost within the node. In other words, the algebraic sum of ALL currents entering and exiting a node must equal zero, i.e., I(exiting) + I(entering) = 0. Kirchhoff’s concept is known as the Conservation of Charge.
Kirchhoff’s first law is also known as Kirchhoff’s Current Law (KCL), Kirchhoff’s Junction Rule (KJR), Kirchhoff’s Point Rule (KPR), and Kirchhoff’s Nodal Rule (KNR). It is an application of the principle of electric charge conservation. The law states that the sum of the currents flowing into and out of any circuit junction is equal.
In layman’s terms, KCL is saying that
The sum of all currents entering and leaving a node equals the sum of all currents leaving and entering the node.
We conduct analysis on all nodes based on current inflow and outflow. The node’s current directions are based on the assumed current directions. As long as the assumed current directions are consistent from node to node, the final analysis result will reflect the actual current directions in the circuit.
Also read:
FAQs
1. Mention Kirchhoff’s Current Law.?
Ans: According to Kirchhoff’s Current Law, the total current entering a junction or a node is equal to the charge leaving the node if no charge is lost.
2. What is another name for Kirchhoff’s First Law?
Ans: Kirchhoff’s Current Law is another name for Kirchhoff’s First Law.
3. Mention Kirchhoff’s voltage law.?
Ans: Kirchhoff’s voltage law states that for any closed network, the voltage around a loop equals the sum of all voltage drops in the same loop and also equals zero.



