Table of Contents
Position Vectors and Displacement Vectors: We came across upward or downward motion, as well as a motion to the left or right of the previously chosen origin, while studying one-dimensional motion. We also gave a positive sign to the right (or upward) and a negative sign to the left (or downward motion). We discussed positive and negative displacements, positive and negative velocities, and positive and negative accelerations in this context.
As a result, in one-dimensional motion, the concept of direction was constrained, and we could only discuss it using positive and negative numbers for displacement, velocity, and acceleration. When describing two- or three-dimensional motions, however, the concept of direction takes on a new meaning.
This is owing to the fact that a particle can have displacement, velocity, or acceleration in multiple directions in two and three dimensions. The concept of vectors must be introduced to deal with such a circumstance.
With that said let’s begin with today’s topic which is
Position and Displacement vectors
In this article we learned, the position vector of an object at time t is the object’s position in relation to the origin. A straight line connecting the origin and the position at time t is used to depict it. The displacement vector of an item between two positions is the straight line that connects the two points, regardless of the path taken.
The displacement is always equal to or larger than the path length. Stay tuned for more such content ahead! We came across upward or downward motion, as well as motion to the left or right of the previously chosen origin, while studying one-dimensional motion. We also gave a positive sign to the right (or upward) and a negative sign to the left (or downward motion). We discussed positive and negative displacements, positive and negative velocities, and positive and negative accelerations in this context.
Get the most Important Questions of Physics, Chemistry, Maths and Biology
Position Vector
Position vectors represent the location of a moving point relative to a body by using a straight line with one end attached to it and the other to the body. The position vector will change length, direction, or both length and direction as the point moves.
When a position vector is drawn to a scale, a change in length indicates a change in magnitude, while a change in direction indicates a rotation of the vector. A position vector can only experience changes in magnitude and direction, and the velocity of the point is defined as the time rate of change of the position vector.
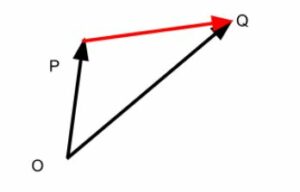
In the picture above, the particle’s position vector when it is at point P is OP, and when it is at point Q is OQ.
Displacement Vector
The displacement vector is defined as the change in an object’s position vector.
Only the starting and ending position vectors affect the displacement vector. When an object follows a path and returns to its original position, the displacement is regarded to be zero.
How to Find a Position Vector?
We must first identify the coordinates of a point before we can determine its position vector. Let’s say we have two points, M and N
And let’s say M and N have (x1, y1) (x2, y2) as their coordinates respectively
And let’s say we are required to find position vector from point M to the point N
We subtract the corresponding components of M from N to get this position vector:
Therefore MN=(x2–x1), (y2–y1)
Let us have a more clear understanding of position and displacement vector by looking into some examples
Position and Displacement of vectors examples (Solved)
Question 1: Determine the position vector AB given two points A = (-3, 4) and B = (6, 12). Determine the magnitude of vector AB.
Solution: We need to find position vector AB
We know the formula, MN=(x2–x1), (y2–y1)
Therefore, AB=[6-(-3)], (12-4)
MN = 9, 8
Now Magnitude of MN= 92+82
81+64=145
Question 2: Determine the position vector PQ given two points P = (-2, -4) and Q = (6, -2). Find the magnitude of the vector AB.
Solution: We need to find position vector AB
We know the formula, MN=(x2–x1), (y2–y1)
Therefore, PQ=[6-(-2)], [(-2-(-4)]
PQ = 8, 2
Now Magnitude of PQ= 82+22
64+4=68
Question 3: The position vector of a particle traveling in a plane is given as
r = x2i+y3j
Calculate the displacement between x = 1 and x = 4 seconds.
Solution: As mentioned above, Displacement only depends upon initial and final position
Therefore r = x2i+y3j at x = 1
= i+j
And similarly r = x2i+y3j at x = 4
=16i+64j
The difference in their position vectors will determine the displacement between them.
Displacement = rfinal–rinitial
(16i+64j)-(i+j)
15i-63j
Question 4: The position vector of a particle traveling in a plane is given as
r = x3i+y4j
Calculate the displacement between x = 2 and x = 6 seconds.
Solution: As mentioned above, Displacement only depends upon initial and final position
Therefore r = x3i+y4j at x = 2
= 8i+16j
And similarly r = x3i+y4j at x = 6
=216i+1296j
The difference in their position vectors will determine the displacement between them.
Displacement = rfinal-rinitial
(216i+1296j)-(8i+16j)
208i-1280j
Also read: Uniformly Accelerated Motion
FAQ’s
Question 1: What does a position vector represent?
Answer 1: Position vectors represent a point’s position relative to the body by using straight lines with one end attached to the body and the other to the moving point. A position vector that coincides with the path is the most convenient for a point moving along a straight path; the velocity of the point is equal to the rate at which the magnitude of the vector varies with respect to time, and it will be a vector lying along the line. The most practical position vector for a point moving on a circular path is one that coincides with the radius of the circle; the point’s velocity is equal to the rate at which the vector’s direction changes with respect to time, and it will be a vector at right angles to the position vector.
Question 2: Is there any difference between a position vector and a unit vector?
Answer 2: When a vector is used to define only the direction and has a magnitude of 1, it is considered a unit vector. Because direction does not require magnitude, the magnitude of the unit vector is always 1. A position vector is a vector that represents the position or location of any given point in relation to any arbitrary reference point, such as the origin.
Question 3: Is the position vector the same as the displacement vector?
Answer 3: A displacement vector is not the same as a position vector. The position vector is used to determine where one object is in relation to another. When characterizing a body’s motion, it’s critical to understand its position. A displacement vector, on the other hand, can be described as a change or variation in a given position vector.






