Table of Contents
Introduction:
The ratio of shear stress to that of shear strain is referred to as the shear modulus. It’s also known as the stiffness modulus, and it’s indicated by G or, less typically, S or. The Pascal (Pa) is the SI unit of shear modulus, but quantities are commonly stated in gigapascals (GPa). Shear modulus is measured in pounds per square inch (PSI) or kilo (thousands) pounds per square in English units (ksi).
A solid with a high shear modulus value is highly stiff. To put it another way, deformation requires a lot of force. A low shear modulus value suggests a soft or flexible solid. To distort it, only a small amount of force is required. A fluid is defined as a substance with a zero-shear modulus. Any force causes the surface to deform.
A brief outline:
When it comes to shear, some materials are isotropic, which means that the distortion in accordance to a force is the same irrespective of orientation. Some substances are anisotropy, implying that they react to stress or strain differently based on their configuration. Shear is much more susceptible to anisotropic materials along one axis than the other. Explore the conduct of a wooden block if a force is applied along to the wood grain versus a force applied perpendicular to the grain. Observe how a diamond behaves to a load exerted on it. The distribution of the force in regard to the crystal lattice influences how readily the crystal shears.
The response of a material to a force applied fluctuates with pressure and temperature. Shear modulus in metals often falls as temperature climbs. With increasing pressure, rigidity diminishes. The Mechanical Threshold Stress (MTS) plastic flow stress type, the Nadal and LePoac (NP) shear strength model and the Steinberg-Cochran-Guinan (SCG) shear stiffness prototype are three models used to predict the effects of temperature and humidity on shear modulus. In metals, there is a temperature and pressure range where the rise in shear modulus is linear. Modelling behaviour outside of this area is more difficult.
Important concepts:
One of the measures of dynamic properties of solids is the shear modulus of elasticity. Young’s modulus and bulk modulus are two other elastic moduli. The ratio of shear stress to shear strain in an object is determined by the material’s shear modulus.
The SI unit for this is the pascal or Pa.
M 1 L-1 T-2 is the dimensional formula for shear modulus.
G is the symbol for it.
It is being used to illustrate how a material opposes transverse deformations, however, it’s only useful for tiny deformations before they may return to their original state. This is due to the fact that large shearing forces induce lasting deformations (no longer elastic body).
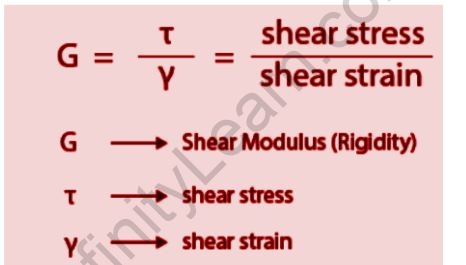
G = τ x y/γ x y
=(FA)/(Δx/l)
= Fl/ AΔx
Units:
- The SI unit pascal, or Pa, is used to measure the modulus of rigidity.
- Giga Pascal is a common measuring unit (GPa).
- It can also be given in psi (pounds per square inch) (PSI).
At the point when a shear power causes horizontal disfigurement, the modulus of inflexibility is the versatile coefficient. It permits us to decide how firm a body is.
Young’s Modulus, Bulk Modulus, and Shear Modulus are unique plans of Hooke’s law, which attests that the strain felt by the relating pressure force is proportional to that pressure for a versatile material. Subsequently, the accompanying condition can be utilized to communicate the connection between versatile constants:
2 G(1+υ) = E = 3 K(1−2υ)
Where,
- Shear Modulus is represented as G
- Young’s Modulus is represented as E
- Bulk Modulus is denoted as K
- Poisson’s Ratio is denoted as υ
Shear modulus is equivalent to the quotient of shear stress divided by shear strain in mathematics. Shear stress is calculated by dividing the shearing force F by the area A parallel to and where it is applied, or F/A. Shear strain, also known as relative deformation, is a measure of change in geometry that is expressed in this case by the trigonometric function tangent (tan) of the angle (theta), which signifies the amount of change in the 90°, or right, angles of the unstrained material’s minute representative cubic volume. Shear strain is mathematically defined as tan or its equivalent, x/y, by definition. The shear modulus can be mathematically stated as
(F/A)/(x/y) = shear modulus = (shear stress)/ (shear strain)
This equation is a variant of Hooke’s elasticity law. The parameters of the shear modulus are those of force per unit area so because the denominator is a ratio and thus dimensionless. The shear modulus is measured in pounds per square inch (commonly shortened to psi) in the English system; the typical SI units are newtons per square metre (N/m2). The shear modulus of aluminium is approximately 3.5 106 psi or 2.4 1010 N/m2. Steel is more than three times as stiff as aluminium when subjected to shear stress.
Significance of shear modulus in NEET exam:
NEET Physics necessitates constant practice as well as a solid grasp of concepts and formulas. To pass the NEET Physics course, you must first learn and master all of the important topics, particularly the modulus section formulae, as specified in the curriculum. It’s the first stage toward solving complicated number problems quickly and easily.
Students perceive numerical physics to be a dream, thus they tend to ignore it and do not practice it sufficiently. As a result, they concentrate on other areas of NEET. This is thought to be the main reason why many people do poorly in NEET Physics, thereby impacting their overall NEET score.
Understudies can utilize the boundless learn site to get part-by-section essential inquiries in a PDF record for additional review. Understudies ought to likewise audit the CBSE prospectus for shear modulus and download related inquiries for each subject. This will make it a lot simpler for everybody to detect any mistakes in their appreciation of their thoughts. Understudies in class 11 should work on modulus resolving key inquiries consistently to support their grades.
Also read: Young’s Modulus
Frequently asked questions:
Question 1: How does the shear modulus change as the imposed shear force increases?
Answer: Whenever the shear force is greater, the shear modulus increases as well.
Question 2: Material 1 has a shear modulus of x pascals, while Material 2 has a shear modulus of 30x pascals. What does this imply?
Answer: If Material 1 has a shear modulus of x pascals and Material 2 has a shear modulus of 30x pascals. Material 2 is, therefore, stiffer than material 1.
Question 3: What is Shear Strain, and what does it imply?
Answer: The strain is the measurement of a body’s deformation in the direction of the applied force.



