Table of Contents
CBSE Previous Year Question Papers Class 10 Maths SA2 Outside Delhi 2016
Time allowed: 3 hours Maximum marks: 90
GENERAL INSTRUCTIONS:
- All questions are compulsory.
- The Question Taper consists of 31 questions divided into four Sections A, B. C. and D.
- Section A contains 4 questions of 1 mark each. Section B contains 6 questions of 2 marks each, Section C contains 10 questions of 3 marks each and Section D contains 11 questions of 4 marks each.
- Use of calculators is not permitted.
SET I
SECTION A
Questions number 1 to 4 carry 1 mark each.
Question 1. In Fig. 1, PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°. Find ∠PCA.
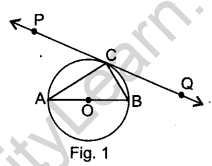
Answer.

Question 2. For what value of k will k + 9, 2k – 1 and 2k + 7 are the consecutive terms of an A.P.?
Answer.
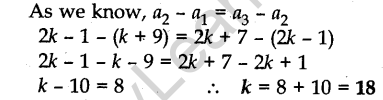
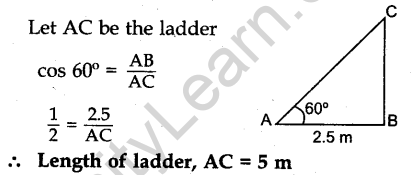
Question 3. A ladder, leaning against a wall, makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
Answer.
Question 4. A card is drawn at random from a well shuffled pack of 52 playing cards. Find the probability of getting neither a red card nor a queen.
Answer.

SECTION B
Questions number 5 to 10 carry 2 marks each.
Question 5. If -5 is a root of the quadratic equation 2x2+ px – 15 = 0 and the quadratic equation p(x2 + x) + k = 0 has equal roots, find the value of k.
Answer.

Question 6. Let P and Q be the points of trisection of the line segment joining the points A (2, -2) and B (-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
Answer.


Question 7. In Fig. 2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that: AB + CD = BC + DA.
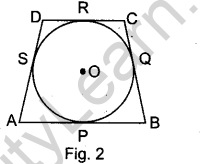
Answer.

Question 8. Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right angled isosceles triangle.
Answer.

Question 9. The 4th term of an A.P. is zero. Prove that the 25th term of the A.P. is three times its 11th term.
Answer.
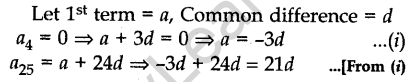
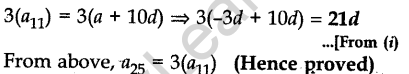
Question 10. In Fig. 3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠OTS = ∠OST = 30°.
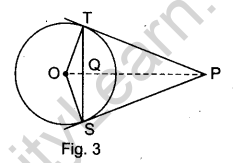
Answer.

SECTION C
Questions number 11 to 20 carry 3 marks each.
Question 11. In Fig. 4, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
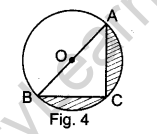
Answer.

Question 12. In Fig. 5, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of Rs 500/sq. metre. (Use π = 22/7 )
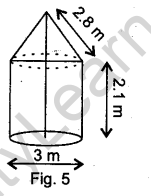
Answer.


Question 13. If the point P(x, y) is equidistant from the points A (a + b,b – a) and B(a -b,a + b), prove that bx = ay.
Answer.

Question 14. In Fig. 6, find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC = 40°. (Use π= 22/7 )
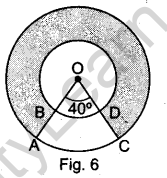
Answer.

Question 15. If the ratio of the sum of first n terms of two A.P’s is (7n + 1) : (4n + 27), find the ratio of their mth terms.
Answer.


Question 16. Solve for x:
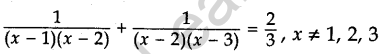
Answer.
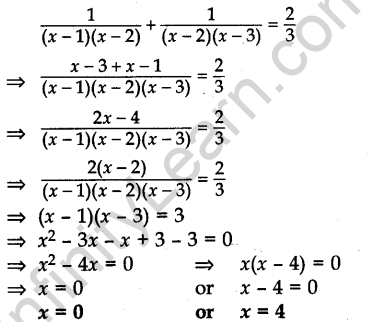
Question 17. A conical vessel, with bash radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. (Use π= 22/7)
Answer.

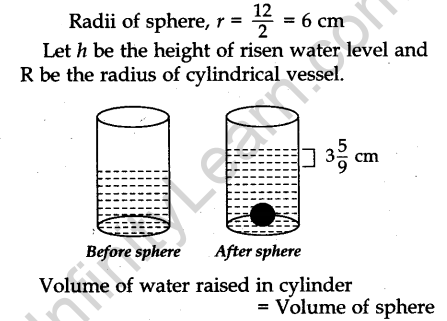
Question 18. A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3 (5/9) cm. Find the diameter of the cylindrical vessel.
Answer.

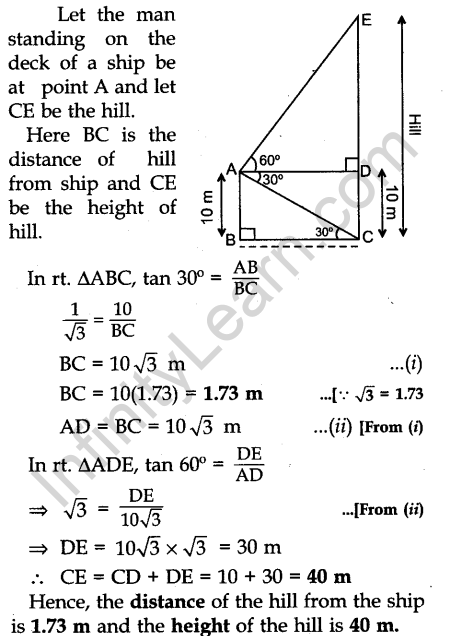
Question 19. A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of hill as 30°. Find the distance of the hill from the ship and the height of the hill.
Answer.
Question 20. Three different coins are tossed together. Find the probability of getting (i) exactly two heads (ii) at least two heads (ii) at least two tails.
Answer.


SECTION D
Questions number 21 to 31 carry 4 marks each.
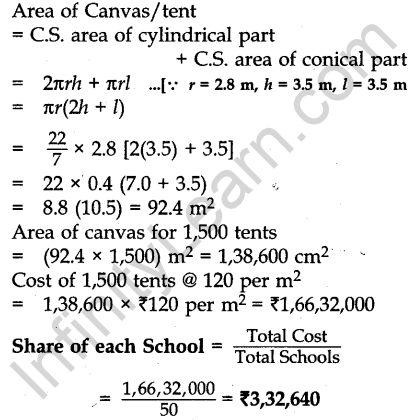
Question 21. Due to heavy floods in a State, thousands were rendered homeless. 50 schools collectively offered to the State Government to provide place and the canvas for 1,500 tents to be fixed by the Government and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 m and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (Use π= 22/7)
Answer.

Value: By helping the flood victims the schools are showing concern for humanity.
Question 22. Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Answer. Theorem. See Q. 27, 2011 (1 Delhi).
Question 23. Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60° to each other.
Answer. See Q. 13, 2013 (I O.D.).
Question 24. In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of DO’/CO.
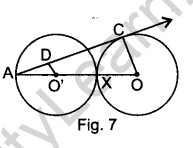
Answer. Given: two equal circles, with centres O and O’, touch each other at point X. OO’ is produced to meet the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC.

Question 25. Solve for x:
![]()
Answer.

Question 26. The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45°. Find the height of the tower PQ and the distance PX. (Use √3= 1.73)
Answer.
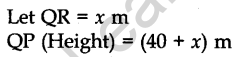


Question 27. The houses in a row are numbered consecutively from 1 to 49. Show that there exists a value of X such that sum of numbers of houses preceding the house numbered X is equal to sum of the numbers of houses following X.
Answer.

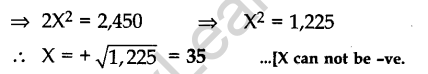
Question 28. In Fig. 8, the vertices of ∆ABC are A(4, 6), B(l, 5) and C(7, 2). A line segment DE is drawn to intersect the sides AB and AC at D and E respectively such that AD/AB= AE/AC= 1/3 .Calculate the area of ∆ADE and Calculate the area compare it with area of ∆ABC.
Answer.


Question 29. A number x is selected at random from the numbers 1, 2, 3 and 4. Another number y is selected at random from the numbers 1, 4, 9 and 16. Find the probability that product of x and y is less than 16.
Answer.

Question 30. In Fig. 9, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r :
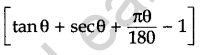
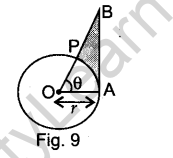
Answer.

Question 31. A motor boat whose speed is 24 km/h in still water takes 1 hr more to go 32 km upstream than to return downstream to the same spot. Find the speed of the stream.
Answer.

SET II
Note:Except for the following questions, all the remaining questions have been asked in Set-I.
Question 10.Solve for x:
![]()
Answer.

Question 18. The digits of a positive number of three digits are in A.P. and their sum is 15. The number obtained by reversing the digits is 594 less than the original number. Find the number.
Answer.

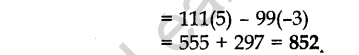
Question 19. If the roots of the quadratic equation (a – b)x2 + (b – c)x + (c – a) = 0 are equal, prove that 2a = b + c.
Answer.
Question 20. From a pack of 52 playing cards, Jacks, Queens and Kings of red colour are removed. From the remaining, a card is drawn at random. Find the probability that drawn card is: (i) a black King (ii) a card of red colour (iii) a card of black colour
Answer.

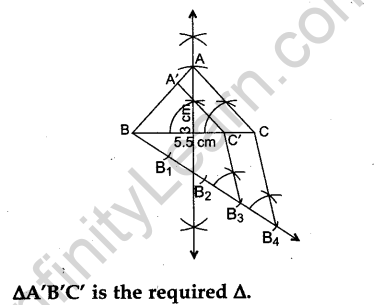
Question 28. Draw an isosceles ∆ABC in which BC = 5.5 cm and altitude AL = 3 cm. Then construct another triangle whose sides are 3/4 of the corresponding sides of ∆ABC.
Answer.
Question 29. Prove that the tangent drawn at any point of a circle is perpendicular to the radius through the point of contact.
Answer. Theorem. See Q. 25, 2011 (I Outside Delhi).
Question 30. As observed from the top of a light house, 100 m high above sea level, the angles of depression of a ship, sailing directly towards it, changes from 30° to 60°. Find the distance travelled by the ship during the period of observation. (Use √3 = 1.73)
Answer.
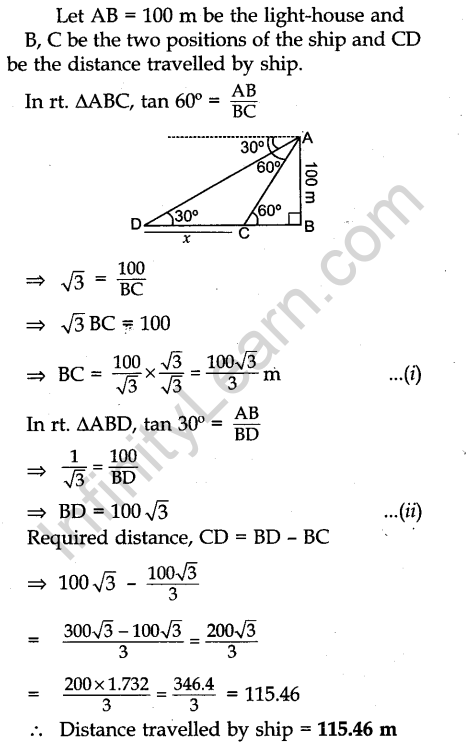
Question 31. A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m. Find the length and breadth of the rectangular park.
Answer.


SET III
Note: Except for the following questions, all the remaining questions have been asked in Set-I and Set II.
Question 10. Solve for x:
![]()
Answer.

Question 18. There are 100 cards in a bag on which numbers from 1 to 100 are written. A card is taken out from the bag at random. Find the probability that the number on the selected card (i) is divisible by 9 and is a perfect square (ii) is a prime number greater than 80.
Answer.

Question 19. Three consecutive natural numbers are such that the square of the middle number exceeds the difference of the squares of the other two by 60. Find the numbers.
Answer.

Question 20. The sums of first n terms of three arithmetic progressions are S1, S2 and S3 respectively. The first term of each A.P. is 1 and their common differences are 1, 2 and 3 respectively. Prove that S1+ S3 = 2S2.
Answer.

Question 28. Two pipes running together can fill a tank in 11 (1/9) minutes. If one pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately.
Answer.


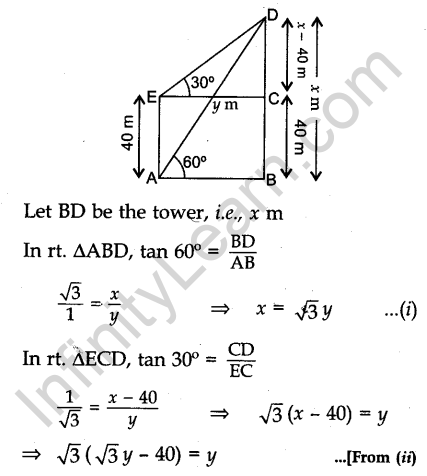
Question 29. From a point on the ground, the angle of elevation of the top of a tower is observed to be 60°. From a point 40 m vertically above the first point of observation, the angle of elevation of the top of the tower is 30°. Find the height of the tower and its horizontal distance from the point of observation.
Answer.

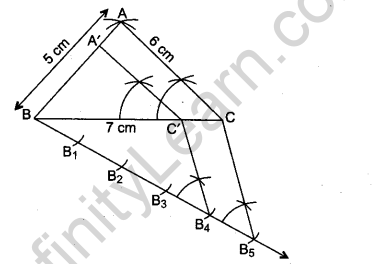
Question 30. Draw a triangle with sides 5 cm, 6 cm and 7 cm. Then draw another triangle whose sides are 4/5 of the corresponding sides of first triangle.
Answer.
Question 31. A number x is selected at random from the numbers 1, 4, 9, 16 and another number y is selected at random from the numbers 1, 2, 3, 4. Find the probability that the value of xy is more than 16.
Answer.




