Table of Contents
- Logic behind Drawing a Perpendicular Bisector of a Line Segment
- Summary
- What’s Next?
In the previous segment of Class 6 Maths, we learnt how to draw a perpendicular bisector of a line segment. Here, let us learn about the logic behind it.
Logic behind drawing a perpendicular bisector of a line segment
The construction of a perpendicular bisector of a line segment is as shown below:
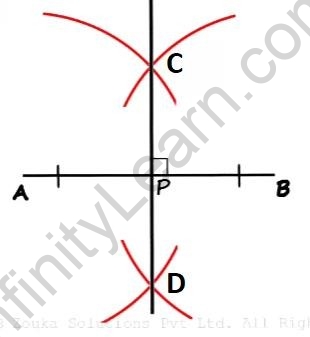
Construction of perpendicular bisector
Let’s understand how the constructed line (line CD) is a perpendicular bisector of the given line
segment (seg AB). That is, to ????? ???? ?? ⊥ ??? ?? ??? ??? ?? ≅ ??? ??.
Join CA, CB, DA, and DB.

Construction for proof
|
No . |
Statement |
Reason |
|
1 |
CA = CB = DA = DB |
The compass width used to draw the arcs was the same. |
|
???????? △ ??? ??? △ ???. |
||
|
2 |
??? ?? ≅ ??? ?? |
From statement 1 |
|
3 |
??? ?? ≅ ??? ?? |
From statement 1 |
|
4 |
??? ?? ≅ ??? ?? |
Common side |
|
5 |
∴△ ??? ≅△ ??? |
By SSS test of congruency. |
|
6 |
∴ ∠??? ≅ ∠??? |
Corresponding angles of congruent triangles are congruent. |
|
7 |
∴ ∠??? ≅ ∠??? |
Corresponding angles of congruent triangles are congruent. |
|
???????? △ ??? |
||
|
8 |
[?????]??? ?? ≅ ??? ??[/?????] |
From statement 1. |
|
9 |
∴ ∠??? ≅ ∠??? |
Opposite angles of congruent sides are congruent in a triangle. |
|
???????? △ ??? |
||
|
10 |
??? ?? ≅ ??? ?? |
From statement 1 |
|
11 |
∴ ∠??? ≅ ∠??? |
Opposite angles of congruent sides |

